Applying the Pythagoras Theorem

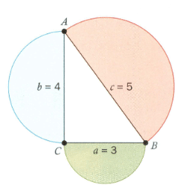
You proved Pythagoras' theorem by constructing squares on each of the sides. Does the formula work with other shapes, for example, circles? If semi-circles are constructed on the sides of a right triangle whose sides measure $3\mathrm{cm},4\mathrm{cm}$ and $5\mathrm{cm}$, show that Pythagoras' theorem still applies.

Groups of three whole numbers that satisfy Pythagoras' theorem are called "Pythagorean triples". Find the third number that would make these into Pythagorean triples. They are given in numerical order.

$\_\_\_, 40, 41$

Groups of three whole numbers that satisfy Pythagoras' theorem are called "Pythagorean triples". Find the third number that would make these into Pythagorean triples. They are given in numerical order.

$8, \_\_\_,17$

Groups of three whole numbers that satisfy Pythagoras' theorem are called "Pythagorean triples". Find the third number that would make these into Pythagorean triples. They are given in numerical order.

$5, 12, \_\_\_$

Groups of three whole numbers that satisfy Pythagoras' theorem are called "Pythagorean triples". Find the third number that would make these into Pythagorean triples. They are given in numerical order.

$3, 4, \_\_\_$

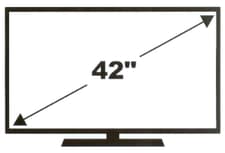
Over the last few decades,television technology has improved, allowing a much wider range of screen sizes.To enable television screen sizes to be easily compared,they are measured using the diagonal of the television.
Suppose you have bought a 42-inch television and the cabinet you want to put it in has a height of 13 inches and a width of 39 inches.Will the television fit in the cabinet?

The heights of two vertical towers are $75 \mathrm{m}$ and $65 \mathrm{m}$. If the shortest distance between the tops of the towers is $61 \mathrm{m}$, how far apart are the middle of the bases of the tower.(If the distance between the middle of the bases of the tower is $k \mathrm{m}$ find the value of $k$ and round off the value up to one decimal place).

Surveying is the science of constructing maps based on measurements. It is a process that cartographers use to calculate heights and distances between different points. A surveyor looks through a theodolite (a measuring device based on a telescope) at a measuring stick that is a known distance away. The telescope's line of sight and the measuring stick form a right-angle. Since the surveyor knows the height of the stick and the horizontal distance to it, she can calculate the length and steepness of a hill or slope.

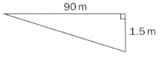
Suppose the horizontal distance between the theodolite and the top of the stick is $90 \mathrm{m}$ and the stick measures $1.5 \mathrm{m}$.
How far is the top of the theodolite from the bottom of the stick? Show your working. (If the distance between the top of the theodolite from the bottom of the stick is $k \mathrm{m}$ find the value of $k$ and round off the value upto one decimal place).

In the construction industry, one-third of all accidents happen while using a ladder. To solve the problem, regulations have been introduced that specify how far the base of the ladder should be from the wall it is leaning against. A ladder measuring $4 \mathrm{m}$ needs to have its base placed $97 \mathrm{cm}$ from the wall. How high up the wall can the ladder reach. (If the height of the wall is $k \mathrm{m}$ find the value of $k$ up to $2$ decimal places).

In the construction industry, one-third of all accidents happen while using a ladder. To solve the problem, regulations have been introduced that specify how far the base of the ladder should be from the wall it is leaning against. If a ladder is to reach a height of $5.6 \mathrm{m}$, the base must be at least $1.4 \mathrm{m}$ from the wall. How long should the ladder be in order to meet this safety regulation. (If the length of the ladder is $k \mathrm{cm}$ find the value of $k$ up to $2$ decimal places).

The diagonals in a square are $10 \mathrm{cm}$ long. Calculate the length of the sides of the square. (If the length of side is $k \mathrm{cm}$ find the value of $k$ upto $2$ decimal places.)

The length of the diagonal of a rectangle is $50 \mathrm{cm}$. If the length of one side of the rectangle is $30 \mathrm{cm}$, Calculate the area of rectangle. (If the area of rectangle is $k {\mathrm{cm}}^2$ find the value of $k$)

The length of the diagonal of a rectangle is $50 \mathrm{cm}$. If the length of one side of the rectangle is $30 \mathrm{cm}$, Calculate the length of other side. (If the length of other side is $k \mathrm{cm}$ find the value of $k$)