Cyclic Quadrilaterals
Important Questions on Cyclic Quadrilaterals
and are chords of a circle which bisect each other. Prove that is a rectangle.
Prove that a cyclic parallelogram is a rectangle.
and are two right triangles with common hypotenuse . Prove that .
If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.
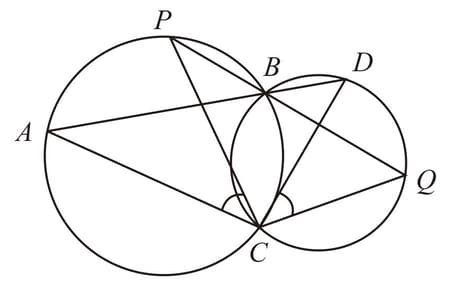
Two circles intersect at two points and Through two line segments and are drawn to intersect the circles at and respectively. Prove that
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.
is a cyclic quadrilateral whose diagonals intersect at a point If is find Further, if find

