Circle Geometry

A quadrilateral is inscribed in a circle of radius $20\sqrt{2}.$ Three of the sides of this quadrilateral have length $20.$ What is the length of the fourth side?

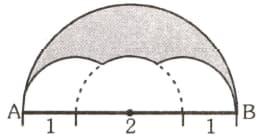
Semicircle $\widehat{AB}$ has center $C$ and radius $1.$ Point $D$ is on $\widehat{AB}$ and $\overline{CD}\perp \overline{AB}.$ Extend $\widehat{BD}$ and $\widehat{AD}$ to $E$ and $F$, respectively, so that circular arcs $\widehat{AE}$ and $\widehat{BF}$ have $B$ and $A$ as their respective centers, circular arc $EF$ has center $D.$ The area of the shaded "smile", $AEFBDA$ is $\left(2\pi -\pi \sqrt{2}-k\right),$ find $k.$

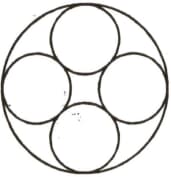
Many cathedrals have windows with portions containing a ring of congruent circles that are circumscribed by a larger circle, In the figure shown, the number of smaller circles is four. If the ratio of the sum of the areas of the four smaller circles to the area of the larger circle is $2\left[x+4y\sqrt{2}\right]$ then find the value of $x^2+y^3$

Circle $A$ has radius $100.$ Circle $B$ has an integer radius $r<100$ and remains internally tangent to circle $A$ as it rolls once around the circumference of circle $A.$ The two circles have the same points of tangency at the beginning and end of circle $B\text{'s}$ trip. How many possible values can $r$ have?

Let $CD$ be a chord of a circle ${\Gamma }_1$ and $AB$ a diameter of ${\Gamma }_1$ perpendicular to $CD$ at $N$ with $AN>NB.$ A circle ${\Gamma }_2$ centred at $C$ with radius  $CN$ intersects ${\Gamma }_1$ at points $P$ and $Q,$ and the segments $PQ$ and $CD$ intersect at $M.$ Given that the radii of ${\Gamma }_1$ and ${\Gamma }_2$ are $61$ units and $60$ units respectively, find the length of $AM.$

Let $A_1, A_2, A_3, A_4, A_5$ and $A_6$ be six points on a circle in this order such that $A_1{A}_2=A_2{A}_3, A_3{A}_4=A_4{A}_5$ and $A_5{ A}_6=A_6{ A}_1,$ where $A_1{ A}_2$ denotes the arc length of the arc $A_1{ A}_2$ etc. It is also known that $\angle A_1{ A}_3{ A}_5=72°.$ Find the size of $\angle A_4{ A}_6{ A}_2$ in degrees.

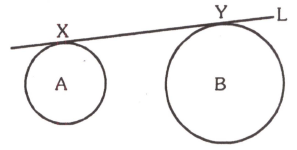
The figure below shows two circles with centres $A$ and $B,$ and a line $L$ which is a tangent to the circles at $X$ and $Y.$ Suppose that $XY=40 \mathrm{cm}, AB=41 \mathrm{cm}$ and the area of the quadrilateral $ABYX$ is $300{ \mathrm{cm}}^2.$ If $a$ and $b$ denote the areas of the circles with centre $A$ and centre $B$, respectively, find the value of $\frac{b}{a}.$

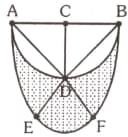
In $∆ABC, \angle CAB=30°$ and $\angle ABC=80°.$ The point $M$ lies inside the triangle such that $\angle MAC=10°$ and $\angle MCA=30°.$ Find the value of $\left(180°-\angle BMC\right)$ in degrees.

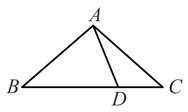
In $∆ABC$ (see below), $AB=AC=\sqrt{3}$ and $D$ is a point on $BC$ such that $AD=1.$ Find the value of $BD·DC.$

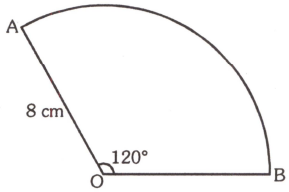
The diagram shows a sector $OAB$ of a circle, centre $O$ and radius $8 \mathrm{cm},$ in which $\angle AOB=120°.$ Another circle of radius $r \mathrm{cm}$ is to be drawn through the points $O, A$ and $B.$ Find the value of $r.$

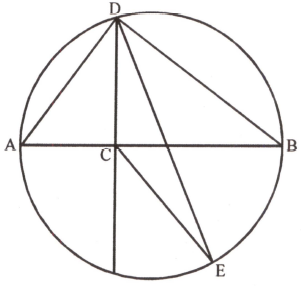
Let $AB$ be a diameter of a circle and $C$ be a point on $AB$ with $2·AC=BC.$ Let $D$ and $E$ be points on the circle such that $DC\perp AB$ and $DE$ is a second diameter. The ratio of the area of $\Delta DCE$ to the area of $∆ABD$ is $\frac{21}{y}.$ What is $y?$

Circle $C_1$ has its center $O$ lying on circle $C_2.$ The two circles meet at $X$ and $Y.$ Point $Z$ in the exterior of $C_1$ lies on circle $C_2$ and $XZ=13, OZ=11,$ and $YZ=7.$ The radius of circle $C_1$ is $\sqrt{R}.$ What is $R?$

The quadrilateral $ABCD$ is inscribed in a circle. The diagonals $AC$ and $BD$ cut at $Q$. The sides $DA$ and $CB$ are produced to meet at $P$. If $CD=CP=DQ$, then the measure of $\angle CAD$ is

In $\Delta ABC, AB=86,$ and $AC=97.$ A circle with centre $A$ and radius $AB$ intersects $BC$ at points $B$ and $X.$ Moreover $BX$ and $CX$ have integer lengths. What is $BC?$

Quadrilateral $ABCD$ is inscribed inside a circle with $\angle BAC=70°, \angle ADB=40°, AD=4,$ and $BC=6.$ What is ${\left(AC\right)}^2?$

Circles with centres $P, Q$ and $R,$ having radii $1, 2$ and $3,$ respectively, lie on the same side of line $\ell$ and are tangent to $\ell$ at $P^{\text{'}}, Q^{\text{'}}$ and $R^{\text{'}},$ respectively, with $Q^{\text{'}}$ between $P^{\text{'}}$ and $R^{\text{'}}.$ The circle with centre $Q$ is externally tangent to each of the other two circles. The area of triangle $PQR$ is $\sqrt{a}-\sqrt{b}.$ What is $a^2+b^2$?

The diameter $AB$ of a circle of radius $2$ is extended to a point $D$ outside the circle so that $BD=3.$ Point $E$ is chosen so that $ED=5$ and the line $ED$ is perpendicular to the line $AD$. Segment $AF$ intersects the circle at point $C$ between $A$ and $E.$ The area of $∆ABC$ is $\frac{P}{S}$, where $P$ and $S$ are co-prime. What is $P-2S?$

A triangle with sides of $5, 12$ and $13$ units has both an inscribed and a circumscribed circle. Find square of twice the distance between the centres of those circles?

A triangle $∆ABC$ has its vertices lying on a circle $C$ of radius $1,$ with $\angle BAC=60°.$ A circle with center $I$ is inscribed in $∆ABC.$ The line $AI$ meets circle $C$ again at $D\mathit{.}$ Find the length of the segment $ID.$

Three semicircles of radius $1$ are constructed on diameter $AB$ of a semicircle of radius $2.$ The centers of the small semicircles divide $\overline{AB}$ into four line segments of equal length, as shown. If the area of the shaded region that lies within the large semicircle but outside the smaller semicircles is $\frac{7\pi -\mathrm{a}\sqrt{3}}{6},$ then value of $a=?$