Second Law of Thermodynamics

In a cold storage, ice melts at the rate of $2 \mathrm{kg} {\mathrm{h}}^{-1}$ when the external temperature is $20°\mathrm{C}$. Find the minimum power output of the motor used to drive the refrigerator which just prevents the ice from melting. Latent heat of fusion of ice $=80 \mathrm{cal} {\mathrm{g}}^{-1}$

A Carnot heat engine has an efficiency of $10\%$. If the same engine is worked backward to obtain a refrigerator, then find its coefficient of performance.

In which case will the efficiency of a Carnot cycle be higher?

(a) When the temperature of the source is increased by $\mathrm{\Delta }T$.

(b) When the temperature of the sink is lowered by $\mathrm{\Delta }T$?

The efficiency of a Carnot cycle is$\frac{1}{6}$. By lowering the temperature of the sink$65 \mathrm{K}$, it increases too$\frac{1}{3}$. Calculate the initial and final temperatures of the sink.

A Carnot engine is designed to operate between $480 \mathrm{K}$ and $300 \mathrm{K}$. Assuming that the engine actually produces $1.2 \mathrm{kJ}$ of mechanical energy per kcal of heat absorbed, compare the actual efficiency with the theoretical maximum efficiency.

A refrigerator whose coefficient of performance is $5$, extracts heat from the cooling compartment at the rate of $250 \mathrm{J}/\mathrm{cycle}$.

(a) How much work per cycle is required to operate the refrigerator?

(b) How much heat is discharged to the room?

A refrigerator freezes water at $0°\mathrm{C}$ into $10 \mathrm{kg}$ ice at $0°\mathrm{C}$ in a time interval of $30 \min$. Assuming the room temperature to be $20°\mathrm{C}$, calculate the minimum amount of power needed to make $10 \mathrm{kg}$ of ice

A heat engine receives $50 \mathrm{kcal}$ of heat from the source per cycle, and operates with an efficiency of $20\%$. Determine the work obtained from the engine and the heat rejected to the sink, per cycle.

During the process $\mathrm{AB}$ of an ideal gas

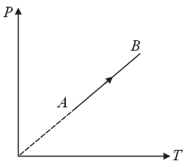
An ideal gas ($1 \mathrm{mol}$, monatomic) is in the initial state $\mathrm{P}$ (see the given figure) on an isothermal $\mathrm{A}$ at temperature ${\mathrm{T}}_0$. It is brought under a constant volume $\left(2{\mathrm{V}}_0\right)$ process to $\mathrm{Q}$ which lies on an adiabatic $\mathrm{B}$ intersecting the isothermal $\mathrm{A}$ at $\left({\mathrm{P}}_0, {\mathrm{V}}_0, {\mathrm{T}}_0\right)$. The change in the internal energy of the gas during the process is (in terms of ${\mathrm{T}}_0$) $\left(2^{2/3}=1.587\right)$

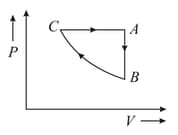
A sample of an ideal gas is taken through the cyclic process $ABCA$ shown in the given figure. It rejects $50 \mathrm{J}$ of heat during the part $AB$, does not absorb or reject the heat during $BC$, and accepts $70 \mathrm{J}$ of heat during $CA$. Forty joules of work is done on the gas during the part $B C$. The internal energy at point $A\left(U_A\right)$ is $1500 \mathrm{J}$. The internal energies at $B$ and $C$. respectively, will be

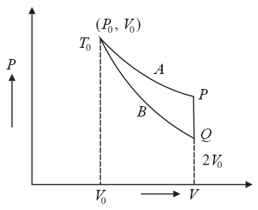
A carnot engine, whose efficiency is $40\%$, takes in heat from a source maintained at a temperature of $500 \mathrm{K}$. It is desired to have an engine of efficiency $60\%$. Then, the intake temperature for the same exhaust (sink) temperature must be

A carnot engine operating between temperatures $T_1$ and $T_2$ has efficiency $\frac{1}{6}$. When $T_2$ is lowered by $62 \mathrm{K}$, its efficiency increases to $\frac{1}{3}$. Then $T_1$ and $T_2$ are, respectively

A solid body of constant heat capacity $1 \mathrm{J} {}^{\circ }\mathrm{C}^{-1}$ is being heated by keeping it in contact with reservoirs in two ways
(i) Sequentially keeping in contact with $2$ reservoirs such that each reservoir supplies the same amount of heat.
(ii) Sequentially keeping in contact with $8$ reservoirs such that each reservoir supplies the same amount of heat.

In both the cases, the body is brought from initial temperature $100 °\mathrm{C}$ to final temperature $200 °\mathrm{C}$. Entropy change of the body in the two cases respectively, is

A reversible engine converts one-sixth of heat absorbed at the source into work. When the temperature of the sink is reduced by $82°\mathrm{C}$, the efficiency of the engine is doubled. Find the temperatures of the source and the sink.

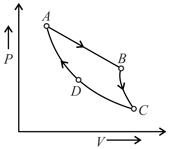
The given figure shows the $P-V$ diagram for a Carnot cycle. In this diagram,