Superposition Principle
Important Questions on Superposition Principle
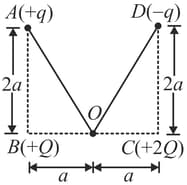
Three charged particles are in equilibrium under their electrostatic forces only.
A ball at is in equilibrium as it is attached with two strings and which are tied at and . The charges at and are and respectively. Find the correct options. The ball at is positively charged.
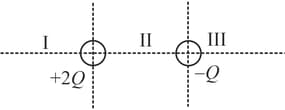
The figure shows two-point charges and . The charges divide the line joining them into three parts , and .
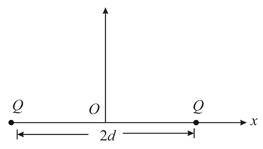
Consider two identical charges placed distance apart, along the -axis (see figure). The equilibrium of a positive test charge placed at point midway between them is,
In arrangement shown in figure, two positive charges, each are fixed. Mark the correct statement (s) regarding a third charged particle placed at the midpoint that can be displaced along or perpendicular to the line connecting the charges.
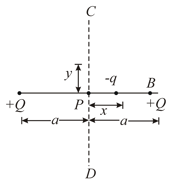
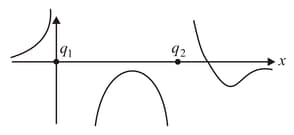
Two points charges ( each) are placed at and A point charge of the same polarity can move along the -axis. Then
Two charges and are kept on the -axis and the electric field at different points on the -axis is plotted against Choose the correct statement about the nature and magnitude of and
Four charges and of same magnitude are fixed along the axis at and respectively. positive charge is placed on the positive axis at a distance Four options of the signs of these charges are given in List I. The direction of the forces on the charge is given in List II. Match List I with List II and select the correct answer using the code given below the lists.
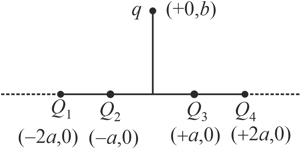
| List I | List II | ||
| P. | all positive | 1. | |
| Q. | positive; negative | 2. | |
| R. | positive; negative | 3. | |
| S. | positive; negative | 4. | |
A charge is placed at each of the opposite corners of a square. A charge is placed at each of the other two corners. If the net electrical force on is zero, then the equals
The corners , , and of a square are occupied by charges , , and , respectively. The side of the square is . The field at the midpoint of a side is zero. What is the value of ?
Given are four arrangements of three fixed electric charges. In each arrangement, a point labelled is also identified. A test charge is placed at . All the charges are of the same magnitude , but they can be either positive or negative as indicated. The charges and point all lie on a straight line. The distances between adjacent items, either between two charges or between a charge and point , are all the same.
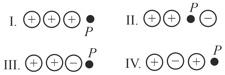
The correct order of choices in decreasing order of magnitude of the force on the is
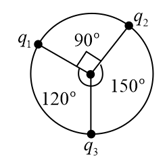
Three positive point charges , and from an isolated system. Suppose the charges have generated a property due to which like charges also attract. The charges are moving along a circle with the same speed maintaining angles as shown in the figure. The charge experiences a force due to the other two charges. Similarly, experiences a force and , a force .
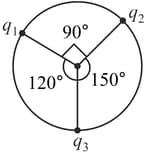
Three positive point charges , and from an isolated system. Suppose the charges have generated a property due to which like charges also attract. The charges are moving along a circle with the same speed maintaining angles as shown in the figure. The charge experiences a force due to the other two charges. Similarly, experiences a force and , a force . The ratio is
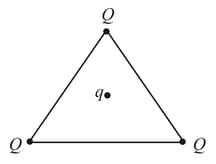
A point charge is placed at the centroid of an equilateral triangle. When a second charge is placed at a vertex of the triangle, the magnitude of the electrostatic force on the central charge is . The magnitude of the net force on the central charge when a third charge is placed at another vertex of the triangle is
Three charges (each ) are placed at the three corners of an equilateral triangle. A fourth charge is placed at the centre of the triangle. The ratio so as to make the system in equilibrium is
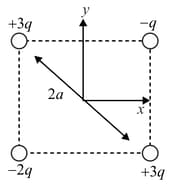
Four point charges are placed at the corners of a square with diagonal as shown. What is the total electric field at the center of the square?
Four identical charges are fixed at the four corners of a square of side . The electric field at a point located symmetrically at a distance from the centre of the square is
It is required to hold equal charges in equilibrium at the corners of a square. What charge when placed at the centre of the square will do this?
Five point charges, each of value , are placed on five vertices of a regular hexagon of side . The magnitude of the force on a point charge of value coulomb placed at the center of the hexagon is
Three positive charges of equal magnitude are placed at the vertices of an equilateral triangle of side . How can the system of charges be placed in equilibrium?

