Sarvesh K Verma Solutions for Chapter: Geometry, Exercise 7: Test of Your Learning
Sarvesh K Verma Quantitative Aptitude Solutions for Exercise - Sarvesh K Verma Solutions for Chapter: Geometry, Exercise 7: Test of Your Learning
Attempt the free practice questions on Chapter 12: Geometry, Exercise 7: Test of Your Learning with hints and solutions to strengthen your understanding. Quantum CAT Also Useful for XAT | SNAP | CMAT | MAT solutions are prepared by Experienced Embibe Experts.
Questions from Sarvesh K Verma Solutions for Chapter: Geometry, Exercise 7: Test of Your Learning with Hints & Solutions
In the following figure and are the four vertices of the square and and are the four mid-points of the sides of the square If each side of the square be then how many of the following statements are correct about the octagon formed at the centre by joining the mid-points with the opposite vertices?
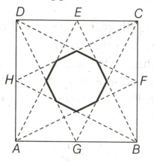
It's an equiangular octagon
It's an equilateral octagon
It's a regular octagon
(IV) it's each side is
(v) it's each side is
A straight line through the vertex of a triangle intersects the side at the point and the circumcircle of the triangle at the point If is not the centre of the circumcircle, then
Let be a square of side length units. Let be the incircle and be the circumcircle of the square . If is a point on and is a point on , the value of is
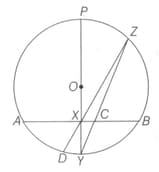
In a circle with centre the diameter is perpendicular to chord as shown in the following figure. Find the correct relation between and
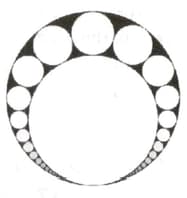
In the following diagram, a circle of radius unit is internally tangent to another circle of radius unit. The region between these two circles is shaded in black. Within the shaded region, there are numerous circles inscribed in such a way that each such triangle is tangent to at least other triangles. If there are total circles drawn in the shaded region, while maintaining the symmetricity, find the sum of curvatures of all the circles.
A circle with diameter is tangent to -axis at and the other circle with diameter is tangent to -axis at Moreover, these two circles are on the same side of -axis and tangent to each other. There is another circle which is tangent to both of these circles and tangent to -axis. Find, the distance between the -axis and the point of tangent of the circle on -axis.
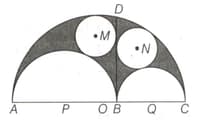
In the following diagram a semicircle with centre $O$ inscribes two semicircles with centers and which are tangent to each other at a point on the diameter of the larger semicircle. and are the diameters of the inscribed semicircles, respectively. A perpendicular is drawn from to is a point on the largest semicircle. There are two circles with centre and inscribed on the different sides of such that these circles are tangent to as well as tangent to an inscribed semicircle and the largest semicircle. If the radii of these circles and be and respectively, which of the followings is/are correct?
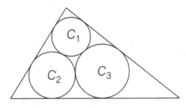
There are three circles inscribed in a triangle such that each circle is tangent to the other two circles and the two sides of the triangle. Let and be the radii or circles and find the inradius of the triangle inscribing these three circles.