An equilateral triangle of side $12 \mathrm{cm}$ is inscribed in a circle. Find the radius of the circle.

On the circle with center $O$, points $A,B$ are such that $OA = AB$. A point $C$ is located on the tangent at $B$ to the circle such that $A$ and $C$ are on the opposite sides of the line $OB$ and $AB=BC$. The line segment $AC$ intersects the circle again at $F$. Then the ratio $\angle BOF:\angle BOC$ is equal to -

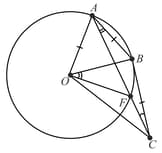
In the given circle, with centre $O$, $\mathrm{K} \mathrm{and} \mathrm{L}$ are the mid-points of equal chords $\text{AB and CD}$ respectively. $\angle OLK=25°$, then the value of $\angle LKB$ is equal to

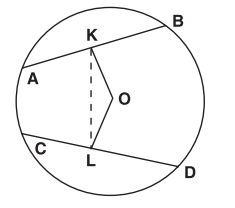
Chords $AB$ and $CD$ are intersecting at $P$. $AB=10$ centimetres, $PB=4$ centimetres and $PD=3$ centimetres. What is the length of $PA$?

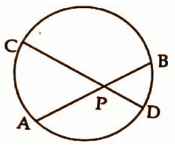
The two chords $AB$ and $CD$ of a circle are at equal distance from the centre $O$. If $\angle AOB=60°$ and $CD=6 cm$, then calculate the length of the radius of the circle.

Draw a chord of length $6 cm$ in a circle of radius $5 cm$. Measure and write the distance of the chord from the centre of the circle.

The length of two chords $AB$ and $CD$ of a circle of centre $O$ are equal and $\angle AOB=60°$ then, $\angle COD$ is

Two parallel chords $AB \text{and} CD$ in a circle are of lengths $8 \mathrm{cm} \text{and} 12 \mathrm{cm}$, respectively and the distance between them is $6 \mathrm{cm}$. The chord $EF$, parallel to $AB \text{and} CD$ and midway between them is of length $\sqrt{k}$, where $k$ is equal to: