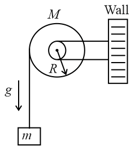
Consider a disc of mass , radius , rotating with angular velocity of about an axis perpendicular to the plane of rotation. An identical disc is kept gently over the rotating disc along the same axis. The energy dissipated so that both the discs continue to rotate together without slipping is _________.
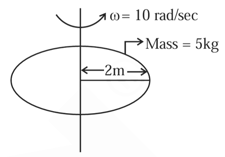

Important Questions on Rotational Motion
A rod of length is pivoted at one end. It is raised such that it makes an angle of from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in ) will be
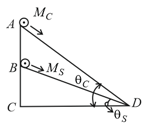
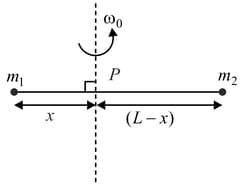
Point masses and are placed at the opposite ends of rigid rod of length , and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity is minimum, is given by:
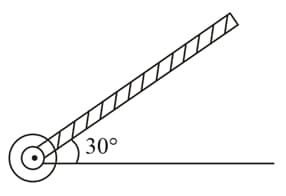
A solid sphere and solid cylinder of identical radii approach an incline with the same linear velocity (see figure). Both roll without slipping all throughout. The two climb maximum heights and on the incline. The ratio is given by:


