The electric field strength depends only on the $x$ and $y$ coordinates according to the law, $\overrightarrow{E}=\frac{ a\left(x\hat{\mathrm{i}}+y\hat{\mathrm{j}}\right)}{\left(x^2+y^2\right)}$ where $a$ is a constant, $\hat{\mathrm{i}} \text{and} \hat{\mathrm{j}}$ are the unit vectors of the $X$ and $Y$ axes. Find the flux of the vector $E$ through a sphere of radius $R$ with its centre at the origin of coordinates. Using the above result, also calculate the total charge enclosed by the sphere.

A positive charge is distributed in a spherical region with charge density $\mathrm{\rho }= {\mathrm{\rho }}_0 \mathrm{r}$ for $\mathrm{r} \le \mathrm{R}$ (where ${\mathrm{\rho }}_0$ is a positive constant and $\mathrm{r}$ is the distance from centre). Find out electric potential and electric field at following locations.

(a) At a distance $\mathrm{r}$ from centre inside the sphere.

(b) At a distance r from centre outside the sphere.

Consider an equilateral triangle $ABC$ of side $2a$ in the plane of the paper as shown. The centroid of the triangle is $O$. Equal charges $\left(Q\right)$ are fixed at the vertices $A, B$ and $C$. In what follows consider all motion and situations to be confined the plane of the paper.

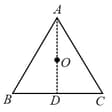
(a) A test charge $\left(q\right)$, of same sign as $Q$, is placed on the median $AD$ at a point at a distance $\delta$ below $O$. Obtain the force $\left(F\right)$ felt by the test charge.
(b) Assuming $\delta \ll a$ discuss the motion of the test charge when it is released.
(c) Obtain the force $\left(F_D\right)$ on this test charge if it is placed at the point $D$ as shown in the figure.
(d) In the figure below mark the approximate locations of the equilibrium point(s) for this system. Justify your answer.
(e) Is the equilibrium at $O$ stable or unstable if we displace the test charge in the direction of $OP$? The line $PQ$ is parallel to the base $BC$. Justify your answer.
(f) Consider a rectangle $ABCD$. Equal charges are fixed at the vertices $A, B, C$ and $D. O$ is the centroid. In the figure below mark the approximate locations of all the neutral points of the system for a test charge with same sign as the charges on the vertices. Dotted lines are drawn for the reference.
(g) How many neutral points are possible for a system in which $N$ charges are placed at the $N$ vertices of a regular $N$ sided polygon ?.

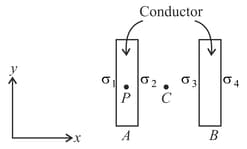
The figure shows two infinitely large conducting plates $A$ and $B$. If the electric field at $C$ due to charge densities ${\mathrm{\sigma }}_1, {\mathrm{\sigma }}_2, {\mathrm{\sigma }}_3$ and ${\sigma }_4$ is $E\hat{\mathrm{i}}$, find ${\mathrm{\sigma }}_2$ and ${\mathrm{\sigma }}_{3 }$in terms of $E$. State whether this much information is sufficient to find ${\mathrm{\sigma }}_1$ and ${\mathrm{\sigma }}_4$ in terms of $E$. Derive a relation between${\mathrm{\sigma }}_1$ and ${\mathrm{\sigma }}_4.$ 

In a neutral conducting hollow sphere of inner and outer radii $5 \mathrm{cm}$ and $10 \mathrm{cm}$ respectively, a point charge $Q=1 \mathrm{C}$ is placed at point $A$, that is $3 \mathrm{cm}$ from the centre $C$ of the hollow sphere. An external uniform electric field of magnitude $20 \mathrm{N} {\mathrm{C}}^{-1}$ is also applied. Net electric force on this charge is $15 \mathrm{N}$, away from the centre of the sphere as shown. Then find:

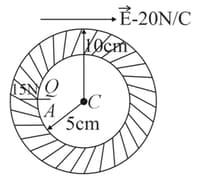
(a) Force due to external electric field on the outer surface of the shell.

(b) Net force on the shell.

(c) Net force on a point charge due to the shell.

A point charge $q$ is brought from infinity (slowly so that heat developed in the shell is negligible) and is placed at the centre of a conducting neutral spherical shell of inner radius $a$ and outer radius $b$, then find work done by external agent.

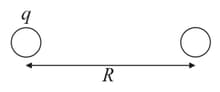
Consider two solid dielectric spheres of radius $\mathrm{a}$, separated by a distance $\mathrm{R}(\mathrm{R}\gg \mathrm{a})$. One of the spheres has a charge $\mathrm{q}$, and the other is neutral (see figure.) We double the distance between two spheres. How much charge should reside on the first sphere now so that the force between the spheres remains the same ?