Theorems of Perpendicular and Parallel Axes

The $\mathrm{M}.\mathrm{I}.$ of solid sphere about an axis passing through its centre is $2\mathrm{kg}-{\mathrm{m}}^2$. Calculate its $\mathrm{M}.\mathrm{I}.$ about a tangent passing through any point on its surface.

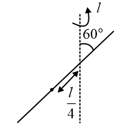
Moment of inertia of a thin uniform rod of length $l$ and mass $m$ about an axis passing through a point at a distance of $\frac{l}{4}$ from centre $O$ and at an angle of $60°$ to the rod is

The radius of gyration of a solid sphere of radius $\mathrm{r}$ about a certain axis is $\mathrm{r}$. Find the distance of this axis from the centre of the sphere.

The moment of inertia of a thin rod of length $L$ and mass $M$ about an axis passing through a point at a distance $\frac{L}{3}$ from one of its ends and perpendicular to the rod is,

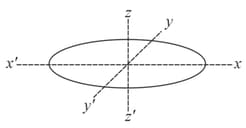
An elliptical disc shown in the figure is rotated in turn about $x-x^{\text{'}},y-y^{\text{'}}$ and $z-z^{\text{'}}$ axes passing through the centre of mass of the disc. Moment of inertia of the disc is

Statement 1 : Moment of inertia of the given rigid body about the two axis will always be same if both the axes are at same distance from centre of mass.

Statement 2 : From parallel axis theorem I = I_cm + md², where all terms have usual meaning.

A square plate is kept in $\mathrm{Y}\mathrm{Z}$ plane. Then according to perpendicular axis theorem

The moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the center of mass and perpendicular the to the axis of the cylinder is ${\mathrm{I1}}_{}$ and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is $I_2$ , then

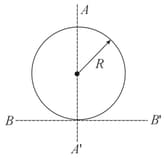
Figure shows a sphere of mass $M$ and radius $R$. Let $AA\text{'}$ and $BB\text{'}$ be two axis as shown in the figure. Then -



Assertion: Parallel axis theorem is not applicable between axis $A{A}^{\mathrm{\prime }}$ and $B{B}^{\mathrm{\prime }}$

Reason: $I_{\mathit{B}{\mathit{B}}^{\mathit{\prime }}}= I_{\mathit{A}{\mathit{A}}^{\mathit{\prime }}}+\mathrm{ }M{R}^2$

The moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is $I_0$. What is the M.I. about an axis through one end and perpendicular to the rod?

If a body is lying in $\mathrm{y}\mathrm{z}$ -plane, then according to the theorem of perpendicular axes the correct expression will be -

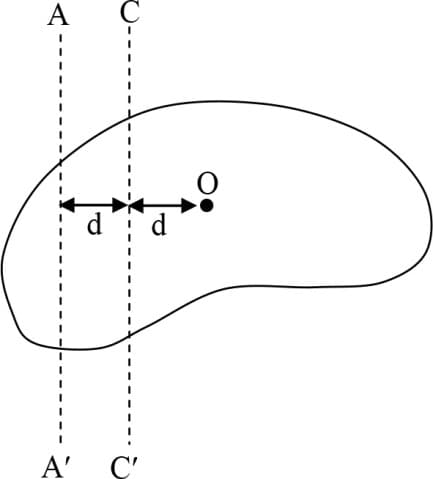
Figure shows a body of arbitrary shape $\mathrm{‘}\mathrm{O}\mathrm{’}$ is the centre of mass of the body and mass of the body is $\mathrm{M}$. If ${\mathrm{I}}_{{\mathrm{C}\mathrm{C}}^{\mathrm{\prime }}}={\mathrm{I}}_0$ then ${\mathrm{I}}_{{\mathrm{A}\mathrm{A}}^{\mathrm{\prime }}}$ will be equal to -

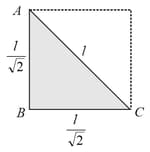
A uniform triangular plate of mass M whose vertices are ABC has lengths l, $\frac{\text{l}}{\sqrt{2}}$ and $\frac{\text{l}}{\sqrt{2}}$ as shown in figure. The moment of inertia of this plate about an axis passing through point A and perpendicular to the plane of the plate is

Moment of inertia of rod of mass $M$ and length $L$ about an axis passing through a point midway between centre and end is

Moment of inertia of a solid cylinder of length $L$ and diameter $D$ about an axis passing through its centre of gravity and perpendicular to its geometric axis is

Let I be the moment of inertia of a uniform square plate about an axis AB that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate that passes through the centre of the plate and makes and angle θ with AB. The moment of inertia of the plate about the axis CD is then equal to

A uniform disc of radius $R$ lies in $x-y$ plane with its centre at the origin. Its moment of inertia about $z$-axis is equal to its moment of inertia about the line $y=x+c$. The value of $c$ is

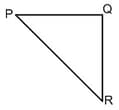
In the triangular sheet given $\text{PQ}=\text{QR}=\ell$. If M is the mass of the sheet,  the moment of inertia about PR is

The moment of inertia of a circular ring about one of its diameters is $I$. What will be its moment of inertia about a tangent parallel to the diameter?