Events

A fair dodecahedral die numbered $1, 2, 3, 4, 8, 9, 16, 27, 32, 81, 243$and $729$ is thrown and the number noted.

The events $C$, "thrown an odd number", and $D$, "throw an event number ", are represented on the venn diagram below:

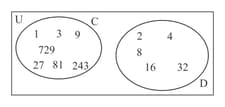
State with a reason whether events $C$ and $D$ are mutually exclusive .

For the given pair of events, state whether they are mutually exclusive, independent or neither.

$C=$it will rain tomorrow

$D=$it is raining today

For the given pair of events, state whether they are mutually exclusive, independent or neither.

$A=$throw a head on a fair coin

$B=$throw a pair number on a fair die numbered $1, 2, 3, 4, 5, 6$

A fair decahedral die numbered $1, 2, 3, ...... 10$ is thrown and the number noted.

The events $A$, 'throw a square number", and $B$, 'throw a factor of six, are represented on the Venn diagram below:

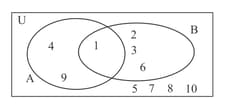
State with a reason whether events $A$ and $B$ are mutually exclusive.

A problem in calculus is given to two students $A$ and $B$, whose chances of solving it are $\frac{1}{3}$ and $\frac{1}{4}$ respectively. If the probability of the problem being solved, if both of them try independently is $\frac{m}{n},$ then $m+n=$

An electronic assembly consists of two sub system, say, $A$ and $B$. When $P$($A$ fails) $= 0.2$, $P$($B$ fails alone) $=0.15$, $P$($A$ and $B$ fail) $=0.15$. Evaluate $P(A \mathrm{fails} \mathrm{alone})$.

$A$ is a set containing $10$ elements. A subset $P$ of $A$ is chosen at random and the set $A$ is reconstructed by replacing the elements of $P$.Another subset $Q$ of $A$ is now chosen at random. Then the probability that if :

$P \& Q$ have no-common elements is

For next three question please follow the same

$A$ is a set containing $10$ elements. A subset $P$ of $A$ is chosen at random and the set $A$ is reconstructed by replacing the elements of $P$.Another subset $Q$ of $A$ is now chosen at random. Then the probability that if :

$\text{P}\cup \text{Q}=\text{A}$ is

A sample space consists of $9$ elementary outcomes $e_1, e_2 ,\dots , e_9$ whose probabilities are

$P\left(e_1\right)=P\left(e_2\right)=.08, P\left(e_3\right)=P\left(e_4\right)=P\left(e_5\right)=.1$

$P\left(e_6\right)=P\left(e_7\right)=.2, P\left(e_8\right)=P\left(e_9\right)=.07$

Suppose $A=\left\{e_1, e_5, e_8\right\}, B=\left\{e_2, e_5, e_8, e_9\right\}$

Calculate $P\left(A\right), P\left(B\right)$ and $P(A\cap B)$

Three coins are tossed once. Let $A$ denote the event ‘three heads show”, $B$ denote the event “two heads and one tail show”, $C$ denote the event” three tails show and $D$ denote the event ‘a head shows on the first coin”. Which events are simple?

The probabilities that Mr. A and Mr. B will die within a year are $\frac{1}{2}$ and $\frac{1}{3}$ respectively, then the probability that only one of them will be alive at the end of the year, is

Two die are thrown simultaneously. The probability of obtaining a total score of $5$ is

If $\frac{1+3p}{3},\frac{1-2p}{2}$ are probabilities of two mutually exclusive events, then p lies in the interval

If $A, B \& C$  are mutually exclusive and exhaustive events of a random experiment such that $P\left(B\right)=\frac{3}{2}P\left(A\right)$ and $P\left(C\right)=\frac{1}{2}P\left(B\right),$ then $P\left(A\cup C\right)$ equals to

The maximum number of possible triangles form by n points in a plane is ${}^n{C}_3.$ Now let us consider a regular octagon. Triangles are formed by joining the vertices of a regular octagon and a triangle is selected. Now given the answers of the following questions.

The probability that the selected triangle has exactly one side common with the sides of octagon is

A man alternately tosses a coin and throws a die beginning with coin. The probability that he gets a head before he gets 5 or 6 on the die is

$A$ and $B$ are to throw $2$ dice. If $A$ throws a sum of $9$ points, then $B^{\text{'}}s$ chance of throwing a higher sum is

A die is loaded such that $6$ turning upwards is twice as often as $1$ and three times as any other face. The chance that we get a face with $1$ point when we throw such a die is

A magical die is so loaded that the probability of any face appearing is proportional to the number of points on its face. The probability of an odd number appearing is