Relations and its Types
Relations and its Types: Overview
This topic covers concepts, such as, Definition of Relations on a Set, Domain, Anti-symmetric Relation on Sets & Inverse of a Relation etc.
Important Questions on Relations and its Types
Let . Find the range of .
Check the relation on the set by is the universal relation.
Let A be the set of all students of a boys school. Show that the relation on given by difference between the heights of and is less than meters} is the universal-relation.
Define universal relation on sets.
Verify the following relation is an identity relation or not:
If and .
If and is the relation on set , then find the antisymmetric relation on set .
In the set of natural numbers, a relation
If and is the relation on set , then find the antisymmetric relation on set .
If and is the relation on set , then find the antisymmetric relation on set .
The diagram shows the graph of a relation that maps set onto set .
Write down as a set of ordered pairs.
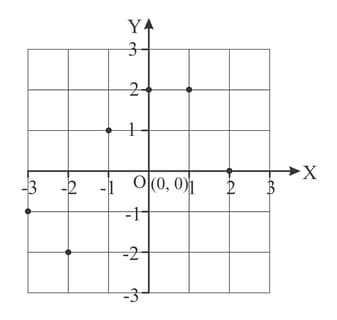
Express the mapping in the form
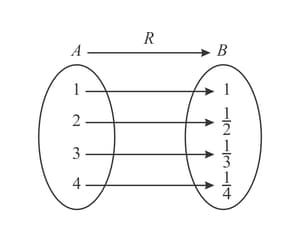
Consider the relation . Classify it as one-to-one, many-to-one, many-to-many or one-to-many.
Consider the relation . Classify it as one-to-one, many-to-one, many-to-many or one-to-many.
Consider the relation . Classify it as one-to-one, many-to-one, many-to-many or one-to-many.
Consider the relation . Classify it as one-to-one, many-to-one, many-to-many or one-to-many.
Consider the relation . Classify it as one-to-one, many-to-one, many-to-many or one-to-many.
Is a function? If is described by , then what value should be assigned to and .
Let and the relation be defined on as follows:
.
Then, write minimum number of ordered pairs to be added in to make reflexive and transitive.
The relation in the set given by is even}, is
Let be a relation on the set of ordered pairs of positive integers defined by if and only if Show that is an equivalence relation.
