Circumference of a Circle
Circumference of a Circle: Overview
In this topic, we will study the significance of the circumference of a circle. It highlights the formula used to find the same and covers various solved examples. It also includes related assorted questions for practice.
Important Questions on Circumference of a Circle
The approximate value of , correct to two decimal places is _____.
The radius of a wheel of an engine is . How many revolutions will it make in travelling ? [Assume ]
Aditya rides the Ferris wheel twice at the Fun Fair. If the radius of the Ferris wheel is , the distance Aditya travelled in two rotations is _____.
(Please use )

Dominos’ large pizza is 14" in diameter. What is the minimum circumference of the pan needed to accommodate this pizza?
(Please use )

The earth has a diameter of . What is the approximate distance you would cover if you could walk around the equator? (Please use )
Freddy, a farmer, has a circular patch of land of boundary of 62.8 m.
There is an electric pole exactly at the centre of the land. If Freddy wants to create a pathway passing right through the electric pole to cross his land then what will be the length of the pathway
(Please use $\pi =3.14$ )
Mahendra made a rhombus using a wire of length 44 cm. Virat took the same wire and bent it to form a circle. The radius of the largest circle that Virat can make is _____ cm.
(Please use $ \pi =\frac{22}{7}$)
Susan has to cut a circle out of a square piece of cardboard to make a clock face. The square piece has a side of 28 cm. If Susan wants to paste a ribbon along the boundary of the circular portion then the minimum length of the ribbon is _____cm.
(Please use $ \pi =\frac{22}{7}$)
The circumference of a circle is 60 cm more than its diameter. Therefore, the radius of the circle is _____cm.
(Please use $ \pi =\frac{22}{7}$)
The difference between the circumference and the diameter of a circle is 30 cm. The radius of the circle is _____cm.
(Please use $ \pi=\frac{22}{7})$
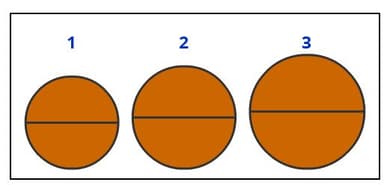
|
Circle |
Radius(r) units |
Diameter(2r) units |
Circumference (C) units |
$ \frac{\text{Circumference}}{\text{Diameter}}=\frac{C}{2r}$ units |
|
1 |
1 |
2 |
6.28 |
3.14 |
|
2 |
2 |
4 |
12.56 |
3.14 |
|
3 |
3 |
6 |
18.84 |
3.14 |
What can you understand from the above?
The ratio of the circumference of two circles is . Find the ratio of their areas.
The diameter of a circle is . If its circumference is , then find the value of . (Take )
The ratio between the circumference of a circle and its diameter is always_____. (Constant/Variable)
Draw five circles of different radii. Now, find out their circumference. Then, find out the ratio of circumference to radius for each circle. Is there any relation between the two quantities? If yes, then what type of relation do they hold? Can we say that 'the circumference of a circle is in direct/inverse variation with its radius'? Can we also find the relation between the area and radius of the circle?
Find the circumference of a circle whose diameter is
(i) 35 cm.
(ii) 4.9 m.
Find the circumference of a circle whose radius is
(i) 28 cm.
(ii) 1.4 m.