Mid-Point Theorem
Important Questions on Mid-Point Theorem
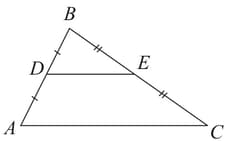
Use mid-segment theorem to name a segment that has twice the length of
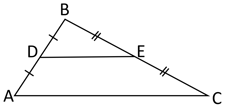
Use mid-segment theorem to name the part of the given triangle: A segment that has half the length of .
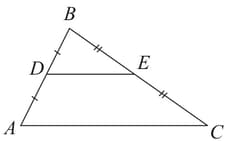
Use mid-segment theorem to name the part of the given triangle: A segment that has the same length as .
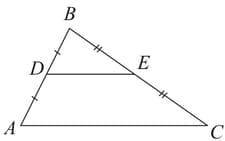
Use mid-segment theorem to name the part of the given triangle: A segment parallel to .
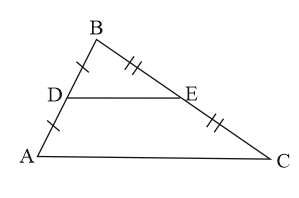
Use mid-segment theorem to name the part of the given triangle: A mid-segment of .
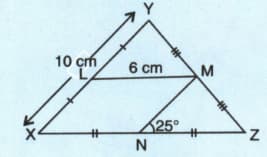
Find the measure of :
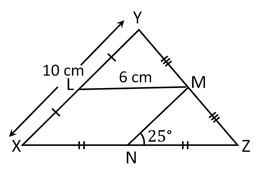
The measure of is . Find the value of .
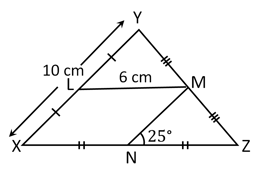
The measure of is . Find the value of .
In the figure given below, is the midpoint of side of a trapezium with A line through parallel to , meets in . Show that is the midpoint of .
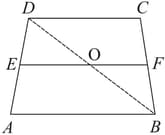
Prove that in a parallelogram, the lines joining a pair of opposite vertices to the mid-points of a pair of opposite sides trisect a diagonal.
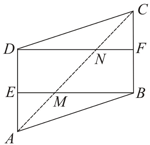
is a parallelogram, is the midpoint of and is the midpoint of . is any line that intersects and in and respectively. Prove that .
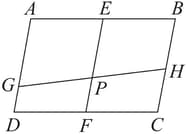
In the quadrilateral the midpoints of are . If it is also given that the diagonals and are equal. What further statement can be made about the parallelogram ?
In the quadrilateral , the midpoints of are . Prove that is a parallelogram.
In the quadrilateral , the midpoints of are . Using the midpoint theorem make a statement concerning the lengths and directions of and .
A quadrilateral is a rhombus and are the midpoints of respectively. Prove that quad. is a rectangle.
Show that the quadrilateral, formed by joining the midpoints of the consecutive sides of a rectangle, is a rhombus.

