Similar Triangles
Important Questions on Similar Triangles
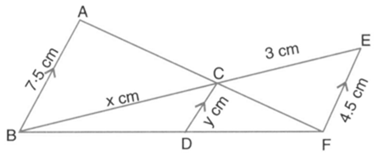
In the following figure, point divides in the ratio Find:
find the length of
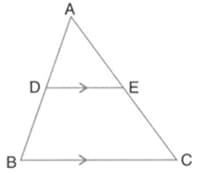
In the following figure, point divides in the ratio Find:
find the length of
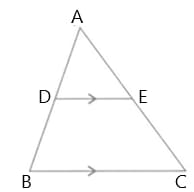
In the following figure, point divides in the ratio Find:
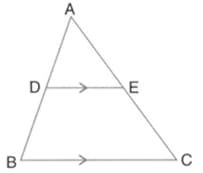
In the given figure, and Find the ratio between areas of the and
In the given figure, is a triangle. is parallel to and
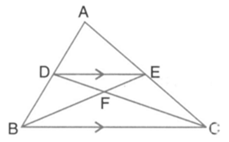
What is ratio of the areas of and ?
In the given figure, is a triangle. is parallel to and
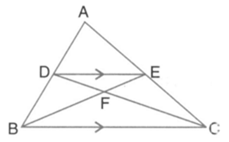
Prove that is similar to
Hence, find
In the given figure, is a triangle. is parallel to and
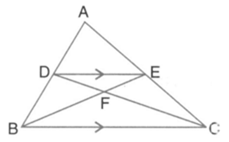
Determine the ratio and
In the given figure, is parallel to Area of triangle Area of trapezium and Calculate the length of
Also, find the area of the triangle
In the figure, given below, is a parallelogram. is a point on such that produced meets produced at Given the area of triangle
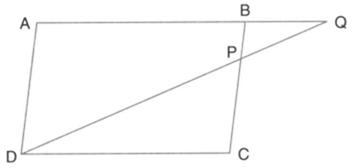
Calculate: Area of parallelogram
In the figure, given below, is a parallelogram. is a point on such that produced meets produced at Given the area of triangle
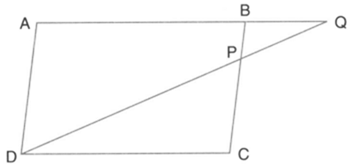
Calculate: Area of triangle
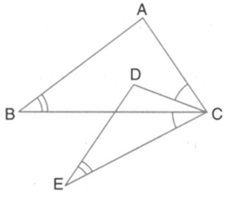
The given diagram shows two isosceles triangles which are similar. In the given diagram, and are not parallel; and
Calculate: The ratio of the areas of triangle and triangle
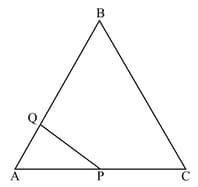
The given diagram shows two isosceles triangles which are similar. In the given diagram, and are not parallel; and
Calculate: The length of
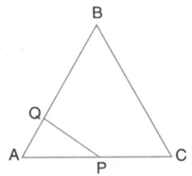
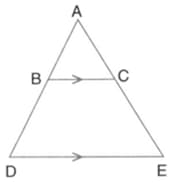
In the given triangle is parallel to and
Calculate the value of ratio:
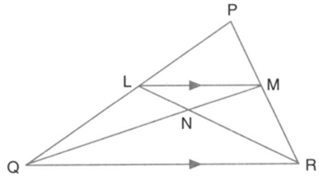
In the given triangle is parallel to and
Calculate the value of ratio:
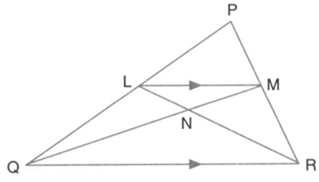
In the given triangle is parallel to and
Calculate the value of ratio: and then
The ratio between the corresponding sides of two similar triangles is is to Find the ratio between the areas of these triangles.
The given figure shows a parallelogram is a point in and produced meets produced at point If and find the perimeter of the parallelogram
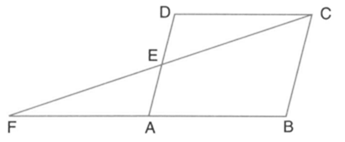
In the following figure, is midpoint of of a parallelogram intersects the diagonal at and produced at Prove that: .
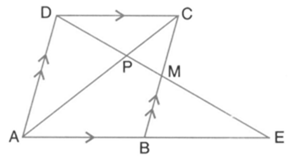
In figure, given below, is a right-angle triangle right angled at is parallel to and Calculate the lengths of and
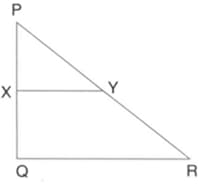
In the figure, given below, and are parallel lines. Given , , , and Calculate the values of and