Angle Bisector Theorem

In a triangle $ABC, X$ and $Y$ are points on the segments $AB$ and $AC$ respectively such that $AX: XB=1:2$ and $AY: YC=2:1.$ If the area of triangle $AXY$ is $10$ then what is the area of triangle $ABC ?$

Areas of two similar triangles are $36 {\mathrm{cm}}^2$and $100 {\mathrm{cm}}^2$. If the length of a side of the larger triangle is $20 \mathrm{cm}$, then the length of the corresponding side of the smaller triangle is

Diagonals of a trapezium $PQRS$ intersect each other at the point $O$. If $PQ\parallel RS \mathrm{and} PQ=3RS$, then the ratio of areas of triangles $POQ \mathrm{and} ROS$ is

$△DEF~△MNK$. If $DE=5$ and $MN=6$, then $\frac{\mathrm{ar}\left(△DEF\right)}{\mathrm{ar}\left(△MNK\right)}=$

The sides of two similar triangles are in the ratio $2:3$, then their areas are in the ratio:

In $∆ABC, XY\parallel BC$ and $XY=\frac{1}{2}BC$. If the area of $△AXY=10 {\mathrm{cm}}^2$, find the area of the trapezium $XYCB$ (in ${\mathrm{cm}}^2$).

$△DEF~△MNK$. If $DE=5$ and $MN=6$, then find the value of $\frac{\mathrm{ar}\left(△DEF\right)}{\mathrm{ar}\left(△MNK\right)}$.

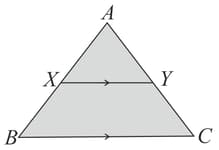
Let $P Q R$ be an acute-angled triangle in which $P Q<Q R$. From the vertex $Q$ draw the altitude $Q{Q}_1$ the angle bisector $Q{Q}_2$ and the median $Q{Q}_3$, with $Q_{1,}{Q}_{2,}{Q}_3$ lying on $P R$. Then,

Let $a, b, c$ be the side-length of a triangle and $l, m, n$ be the lengths of its medians. Put $K=\frac{l+m+n}{a+b+c}$ Then, as $a, b, c$ vary, $K$ can assume every value in the interval

In a triangle $ABC,\angle BAC=90°;AD$ is the altitude from $A$ on to $BC$. Draw $DE$ perpendicular to $AC$ and $DF$ perpendicular to $AB$. Suppose $AB=15$ and $BC=25.$ Then the length of $EF$ is
 

If $△ABC~△DEF$ in which $AB=1.6 \mathrm{cm}, DE=2.4 \mathrm{cm}$. The ratio of the areas of $△ABC \text{and} △DEF$ is

If the ratio of the heights of two similar triangles is $4:9$, find the ratio of the areas.

In $DABC$, $AD$ is the bisector of $\angle A$, also $AB=8 \mathrm{cm}, BD=5 \mathrm{cm}, DC=4 \mathrm{cm}$, find the length of $AC$.

Note: This question given in the book seems to have errors and the modified question should be as below.

Perpendiculars $PB$ and $QA$ are drawn to two ends of a line segment $AB$. If $P$ and $Q$ are at the opposite sides of $AB$ and their joining line intersects $AB$ at $O$. Also $PO=5 \mathrm{cm}, QO=7 \mathrm{cm}, \mathrm{area} ∆POB=150 {\mathrm{cm}}^2$, find the $\mathrm{area} ∆QOA$ in ${\mathrm{cm}}^2$.

In a $∆ABC$, if point $D$ is on the side $BC$ such that $\frac{AB}{AC}=\frac{BD}{DC}$ and $\angle B=70°, \angle C=50°$. Find $\angle BAD$.

Given $∆ABC~∆DEF$, and $AB=10 \mathrm{cm}, DE=8 \mathrm{cm}$, then area of $∆ABC:$area of $∆DEF$ will be:

In a trapezium $ABCD, AD\parallel DC$ and its diagonals intersects each other at $O$. If $AB=2CD$, the ratio of the areas $∆AOB$ and $∆COD$ is:

The areas of two triangles are $25 {\mathrm{cm}}^2$ and $36 {\mathrm{cm}}^2$ respectively. If a median of smaller triangle is $10 \mathrm{cm}$, the corresponding median of larger triangle is:

In figure, if $AB=3.4 \mathrm{cm}, BD=4 \mathrm{cm}, BC=10 \mathrm{cm}$, then the measure of $AC$ is:

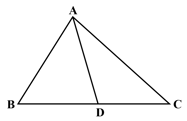
(Note: $\mathrm{AD}$ is the angle bisector of $\mathrm{A}$).

In the figure, $AD$ is the bisector of $\angle A$, if $AB=6 \mathrm{cm}, BD=8 \mathrm{cm}, DC=6 \mathrm{cm}$, then the length of $AC$ will be: