Distance Formula

Find the point on $y\text{-axis}$ which is equidistant from the points $\left(5,-2\right)$ and $\left(-3,2\right)$.

If $A(-2,1), B(a,0), C(4,b)$ and $D(1,2)$ are the vertices of a parallelogram $ABCD,$ find the values of $a$ and $b.$ Hence, find the length of its sides.

Triangle $ABC$ has vertices $A(3,-1), B(-3,-5)$ and $C(-1,5)$. Determine whether the triangle is a right triangle. Fully justify your answer.

Show that the points $\left(2a, 6a\right), \left(2a, 4a\right)$ and $\left(2a+\sqrt{3}a, 5a\right)$ are the vertices of an equilateral triangle of side $2a$ units.

Calculate the distance between the following pair of point.

$\left(5,8\right)$ and $\left(5,-3\right)$

A circle of radius $10$ is drawn with the origin as centre. Check whether each of the points with coordinates $(6, 9), (5, 9), (6, 8)$ is inside, outside or on the circle.

Find the point on the $x-$axis which is equidistant from $(2, -5)$ and $(-2, 9)$.

Find the distance between the following pair of points.
$(-8, 6)$ and $(2, 0)$

Find the distance between the following pair of points
$(7, 8)$ and $(-2, 3)$

In the given figure, $ABC$ is a triangle and $BC$ is parallel to $Y-\mathrm{axis}$. $AB$ and  $AC$ intersect the $Y-\mathrm{axis}$ at $P$ and $Q$, respectively.

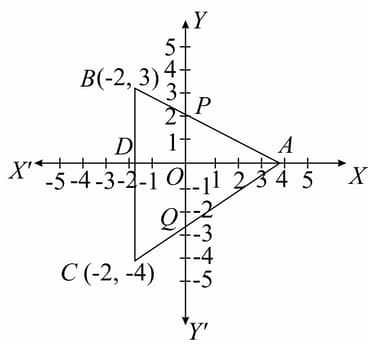
Find the length of $AB \mathrm{and} AC$.

In order to prove the three given points $\mathrm{A}\left(x_1,y_1\right),\mathrm{B}\left(x_2,y_2\right)$ and $\mathrm{C}\left(x_3,y_3\right)$ are the vertices of a right triangle, we need to verify_____theorem.

If points $\mathrm{A}(5,\mathrm{p}), \mathrm{B}(1,5), \mathrm{C}(2,1)$ and $\mathrm{D}(6,2)$ form a square $\mathrm{A}\mathrm{B}\mathrm{C}\mathrm{D}$, then $\mathrm{}\mathrm{p}\mathrm{}=$

The distance between the points $\left(\cos \theta , \sin \theta \right)$ and $(\sin \theta , -\cos \theta )$ is

The nearest point from the origin is

If the distance between the points $\left(4,p\right)$ and $\left(1,0\right)$ is $5$, then the value of $p$ is

The points $\left(-4,0\right),\left(4,0\right),\left(0,3\right)$ are the vertices of a