Scalar Triple Product

Find $\lambda$ such that the four points $A\left(-1, 4, -3\right), B\left(3, \lambda , -5\right), C\left(-3, 8, 5\right)$ and $D\left(-3, 2, 1\right)$ are coplanar.

Find the value of $\lambda$ for which the four points with position vectors $6\hat{i}-7\hat{j}, 16\hat{i}-19\hat{j}-4\hat{k}, \lambda \hat{j}-6\hat{k}$ and $2\hat{i}-5\hat{j}+10\hat{k}$ are coplanar.

Find the value of $\lambda$ for which the four points $A, B, C$ and $D$ with position vectors $-\hat{j}-\hat{k}, 4\hat{i}+5\hat{j}+\lambda \hat{k}, 3\hat{i}+ 9\hat{j}+4\hat{k}$ and $-4\hat{i}+4\hat{j}+4\hat{k}$ respectively are coplanar.

If $\overrightarrow{a}= \hat{i}-\hat{k}$ ,$\overrightarrow{b}= x\hat{i}+ \hat{j}+(1- x)\hat{k}$, $\overrightarrow{c}=y\hat{i}+x\hat{j}+(1+x-y)\hat{k}$ and, then show that$\left[\overrightarrow{a} \overrightarrow{b} \overrightarrow{c}\right]$ is independent of $x$ and $y$ .

If$\overrightarrow{a}=\hat{i}+\hat{j}+\hat{k}$, $\overrightarrow{b}=\hat{i}-\hat{j}+2\hat{k}$, $\overrightarrow{c}=x\hat{i}+(x-2)\hat{j} - \hat{k}$ and the vector $\overrightarrow{c}$ lies in the plane of $\overrightarrow{a}$ and $\overrightarrow{b}$, then find the value of $x$.

Find the value of $\lambda$ so that the vectors $2\hat{i}-\hat{j}+\hat{k}, \hat{i}+2\hat{j}-3\hat{k}$ and $3\hat{i}+\lambda \hat{j}+5\hat{k}$ are coplanar.

Find the value of $\lambda$ so that the vectors $\hat{i}-\hat{j} + \hat{k}, 2\hat{i}+ \hat{j}-\hat{k}, \lambda \hat{i}-\hat{j}+\lambda \hat{k}$ are coplanar.

Find the value of$\lambda$  so that the vectors  $\hat{i}+3\hat{j},5\hat{k}$ and $\lambda \hat{i}-\hat{j}$ are coplanar.

Find the volume of the parallelepiped whose coterminous edges are represented by the vectors $\hat{i}+\hat{j}+ \hat{k}, \hat{i}-\hat{j}+\hat{k}$ and $\hat{i}+2\hat{j}$.

Find the volume of the parallelepiped whose coterminous edges are represented by the vectors $\overrightarrow{a}=2\hat{i}-3\hat{j}+4\hat{k}, \overrightarrow{b}=\hat{i}+2\hat{j}-\hat{k}$ and $\overrightarrow{c}=2\hat{i}-\hat{j}+2\hat{k}$.

If $\overrightarrow{a}=2\hat{i}-3\hat{j}+4\hat{k},$ $\overrightarrow{b}=\hat{i}+2\hat{j}-\hat{k}$ and $\overrightarrow{c}= 3\hat{i}-\hat{j}+2\hat{k},$ then find $\left|\left[\overrightarrow{a}+\overrightarrow{b} \overrightarrow{b}+\overrightarrow{c} \overrightarrow{c}+\overrightarrow{a}\right]\right|$.

If $\overrightarrow{a}=2\hat{i}-3\hat{j}+4\hat{k},$ $\overrightarrow{b}=\hat{i}+2\hat{j}-\hat{k}$ and$\overrightarrow{c}= 3\hat{i}-\hat{j}+2\hat{k},$ then find $\left[\overrightarrow{a} \overrightarrow{b} \overrightarrow{c}\right]$.

If $\overrightarrow{a}=2\hat{i}-3\hat{j}+4\hat{k},$ $\overrightarrow{b}=\hat{i}+2\hat{j}-3\hat{k}$ and $\overrightarrow{c}= 3\hat{i}+4\hat{j}-\hat{k}$, then find $(\overrightarrow{a}\times \overrightarrow{b})·\overrightarrow{c}$ and $\overrightarrow{a}·\left(\overrightarrow{b}\times \overrightarrow{c}\right). \mathrm{Is} \left(\overrightarrow{a}\times \overrightarrow{b}\right)·\overrightarrow{c}=\overrightarrow{a}·\left(\overrightarrow{b}\times \overrightarrow{c}\right)?$

Using scalar triple product, prove that the points $\left(-1, 4, 3\right), \left(3, 2, 5\right), \left(-3, 8, -5\right)$ and $\left(-3, 2, 1\right)$ are coplanar.

If 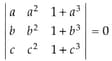 and the vectors $\overrightarrow{A}=(1, a, a^2)$, $\overrightarrow{B}=(1, b, b^2)$, $\overrightarrow{C}=(1, c, c^2)$ are non-coplanar, then prove that $abc = -1$.

If the vectors $\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}$ are coplanar, show that $\overrightarrow{a}+\overrightarrow{b}, \overrightarrow{b}+\overrightarrow{c}, \overrightarrow{c}+\overrightarrow{a}$are also coplanar.

For any three vectors$\overrightarrow{a}, \overrightarrow{b}$ and $\overrightarrow{c}$, show that $\overrightarrow{a}- \overrightarrow{b}, \overrightarrow{b}-\overrightarrow{c}$ and $\overrightarrow{c}-\overrightarrow{a}$ are coplanar.

If $\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}$ are three vectors, show that $(\overrightarrow{a} +\overrightarrow{b}) · \left[\right(\overrightarrow{b}+\overrightarrow{c})\times (\overrightarrow{c}+\overrightarrow{a}) ]= 2[\overrightarrow{a} \overrightarrow{b} \overrightarrow{c}]$

Show that the four points having position vectors $6\hat{i}-7\hat{j}, 16\hat{i}-19\widehat{ j}-4\hat{k}, 3\hat{j}-6\hat{k}$ and $2\hat{i}+ 5\hat{j}+10\hat{k}$ are not coplanar.

Show that the four points with position vectors $4\hat{i}+8\hat{j}+12\hat{k}$, $2\hat{i}+4\hat{j}+6\hat{k}$, $3\hat{i}+5\hat{j}+4\hat{k}$ and $5\hat{i}+8\hat{j}+5\hat{k}$ are coplanar.