Law of Radioactive Decay

Two nuclei have mass numbers in the ratio $1:8$. The ratio of their nuclear radii would be:

How long will a radioactive isotope, whose half life is $T$ years, take for its activity to reduce to ${\left(\frac{1}{8}\right)}^{\mathrm{th}}$ of its initial value?

Two nuclei have mass numbers in the ratio $8 : 125$. The ratio of their nuclear radii is:

Following statements related to radioactivity are given below :
(A) Radioactivity is a random and spontaneous process and is dependent on physical and chemical conditions.
(B) The number of undecayed nuclei in the radioactive sample decays exponentially with time.
(C) Slope of the graph of ${\log }_e$ (no. of undecayed nuclei) vs. time represents the reciprocal of mean life time $\left(\tau \right)$.
(D) Product of decay constant $\left(\lambda \right)$ and half-life time $\left(T_{\frac{1}{2}}\right)$ is not constant.

Choose the most appropriate answer from the options given below: 

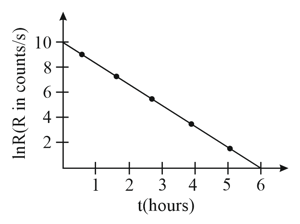
From the given plot of the decay rate $\mathrm{R}$ versus time $t$ of some radioactive nuclei, the half life of the nuclei in hours can be estimated to be

The half-life of ${}_{92}^{238}\mathrm{U}$ undergoing $\alpha -$decay is $4.5\times {10}^9$ $\mathrm{years}$. Calculate the activity of $1 \mathrm{g}$ sample of${}_{92}^{238}\mathrm{U}$. (Avogadro's number is $6.022\times {10}^{23}$)

The ${\beta }^{-}$ activity of a sample of $\mathrm{C}{\mathrm{O}}_2$ prepared from a contemporary wood gave a count rate of $\text{25.5}$ counts per minute $\left(\mathrm{cpm}\right)$. The same mass of $\mathrm{C}{\mathrm{O}}_2$ from an ancient wooden statue gave a count rate of $\text{20.5}$ $\mathrm{cpm}$ under the same conditions. If the half life of ${}^{14}\mathrm{C}$ is $5770 \mathrm{years}$, then the age of the statue is close to [Take ${\log }_{10}\left(\frac{255}{205}\right)\approx 0.095$]

The half-life of a radioactive sample is $T$. If the activities of the sample at a time $t_{\mathrm{1 }}$and $t_2$ $\left(t_1<t_2\right)$ are $R_1$ and $R_2$ respectively, then the number of atoms disintegrated in time $t_2-t_1$ is proportional to

A piece of wood from a recently cut tree shows $20$ decays per minute. A wooden piece of the same size placed in a museum (obtained from a tree cut many years back) shows $2$ decays per minute. If the half-life of ${\mathrm{C}}^{14}$ is $5730 \mathrm{years}$, then the age of the wooden piece placed in the museum is approximately:

The half life of radium is about $1600 \mathrm{years}$. Of $100 \mathrm{g}$ of radium existing now, $25 \mathrm{g}$ will remain unchanged after

Half-lives of two radioactive elements $A$ and $B$ are $20 \mathrm{minutes}$ and $40 \mathrm{minutes}$, respectively. Initially, the samples have an equal number of nuclei. After $80 \mathrm{minutes}$, the ratio of decayed numbers of $A$ and $B$ nuclei will be:

The activity of a radioactive sample is measured as $N_0$ counts per minute at $t=0$ and $\frac{N_0}{e}$, i.e., counts per minute at $t=5$ minutes. The time (in minutes) at which the activity reduces to half its value is,

The half-life period of a radioactive element $X$ is the same as the mean lifetime of another radioactive

If a radioactive substance decays ${\left(\frac{1}{16}\right)}^{\mathrm{th}}$ of its original amount in $2 \mathrm{h}$, then the half-life of that substance is

If the half-life of any sample of a radioactive substance is $4 \mathrm{days}$, then the fraction of sample will remain undecayed after $2 \mathrm{days}$, will be

$n$ $\alpha$-particles per second are being emitted by $N$ atoms as a radioactive element. The half-life of element will be

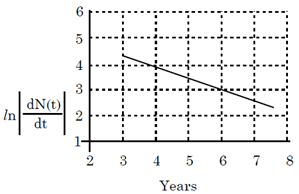
To determine the half-life of a radioactive element, a student plots graph of $ln\left|\frac{\mathrm{d}N\left(t\right)}{\mathrm{d}t }\right| \text{versus} t$. Here $\frac{\mathrm{d}N\left(t\right)}{\mathrm{d}t}$ is the rate of radioactive decay at time $t$. If the number of radioactive nuclei of this element decreases by a factor of $p$ after $4.16 \mathrm{yr}$, the value of $p$ is
$\left(e^{-2.08}=0.125\right)$

A radioactive substance $X$ is being produced at a constant rate $a$ per second. Its decay constant is $b$. The relation between the maximum number of nuclei of $X$ is $N_{\max }=\frac{aK}{b}$, then the value of $K$ is

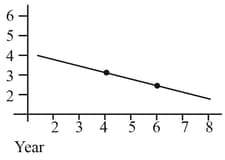
To determine the half life of a radioactive element, a student plots a graph of $\ln \left|\frac{\mathrm{d}N\left(t\right)}{dt}\right|$ versus $t.$ Hence $\frac{dN\left(t\right)}{dt}$ is the rate of radioactive decay at time $t.$ If the number of radioactive nuclei of this element decreases by a factor of $p$ after $4.16$ years, the value of $p$ is: