Calorimetry

A copper cube of mass $200 \mathrm{g}$ slides down a rough inclined plane of inclination $37°$ at a constant speed. Assuming that the loss in mechanical energy goes into the copper block as thermal energy, find the increase in temperature of the block as it slides down through $60 \mathrm{cm}$. Specific heat capacity of copper is equal to $420 \mathrm{J} {\mathrm{kg}}^{-1} {\mathrm{K}}^{-1}$. (Take $\mathrm{g}=10 \mathrm{m} {\mathrm{s}}^{-2}$)

Ice at $0 °\mathrm{C}$ is added to $200 \mathrm{g}$ of water, initially at $70 °\mathrm{C}$ in a vacuum flask. When $50 \mathrm{g}$ of ice has been added and has all melted, the temperature of the flask and contents is $40 °\mathrm{C}$. When a further $80 \mathrm{g}$ of ice has been added and has all melted, the temperature of the whole becomes $10 °\mathrm{C}$. Find the latent heat of fusion of ice.

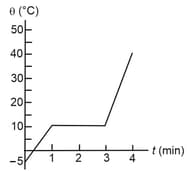
As a physicist, you put heat into a $500 \mathrm{g}$ solid sample at the rate of $10.0 \mathrm{kJ} {\min }^{-1}$, while recording its temperature as a function of time. You plot your data and obtain the graph shown in figure.

(a) What is the latent heat of fusion for this solid?
(b) What is the specific heat of the solid state of the material?

Two liquids of specific heat ratio $1: 2$ are at temperatures $2\mathrm{\theta }$ and $\mathrm{\theta }$.

A kettle with $2 \mathrm{L}$ water at $27 °\mathrm{C}$ is heated by operating a coil heater of power $1 \mathrm{kW}$. The heat is lost to the atmosphere at a constant rate $160 \mathrm{J} {\mathrm{s}}^{-1}$, when its lid is open. In how much time will water be heated to $77 °\mathrm{C}$ with the lid open? (Specific heat of water $=4.2 \mathrm{kJ} °{\mathrm{C}}^{-1} {\mathrm{kg}}^{-1}$)

A ball is dropped on a floor from a height of $2.0 \mathrm{m}$. After the collision, it rises up to a height of $1.5 \mathrm{m}$. Assume that $40 \%$ of the mechanical energy lost goes as thermal energy into the ball. Calculate the rise in the temperature of the ball in the collision. The specific heat of the ball is $800 \mathrm{J} {\mathrm{K}}^{-1}$.

A certain amount of ice is supplied heat at a constant rate for $7 \min$. For the first $1 \min$, the temperature rises uniformly with time. Then, it remains constant for the next $4 \min$, and again the temperature rises at uniform rate for the last $2 \min$. Calculate the final temperature at the end of $7 \min$. (Given: $L$ of ice $=336\times {10}^3 \mathrm{J} {\mathrm{kg}}^{-1}$ and specific heat of water $=4200 \mathrm{J} {\mathrm{kg}}^{-1} {\mathrm{K}}^{-1}$)

In a container of negligible mass, $140 \mathrm{g}$ of ice, initially at $-15 °\mathrm{C}$, is added to $200 \mathrm{g}$ of water that has a temperature of $40 °\mathrm{C}$. If no heat is lost to the surroundings, what is the final temperature of the system and masses of water and ice in the mixture?

A closed thermally insulated vessel contains $100 \mathrm{g}$ of water at $0°\mathrm{C}$. If air from this vessel is rapidly pumped out, intensive evaporation will produce cooling and as a result of this, water freezes. How much ice will be formed by this method, if latent heat of fusion is $80 \mathrm{cal} {\mathrm{g}}^{-1}$ and of evaporation $560 \mathrm{cal} {\mathrm{g}}^{-1}$?

A ball is dropped on a floor from a height of $2.0 \mathrm{m}$. After the collision, it rises up to a height of $1.5 \mathrm{m}$. Assume that $40 \%$ of the mechanical energy lost goes as thermal energy into the ball. Calculate the rise in the temperature of the ball in the collision. The specific heat of the ball is $800 \mathrm{J} {\mathrm{K}}^{-1}$ [Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$].

A lead bullet penetrates into a solid object and melts. Assuming that $50 \%$ of its kinetic energy was used to heat it, calculate the initial speed of the bullet. The initial temperature of the bullet is $27 °\mathrm{C}$ and its melting point is $327 °\mathrm{C}$. Latent heat of fusion of lead$=2.5\times {10}^4 \mathrm{J} {\mathrm{kg}}^{-1}$ and specific heat capacity of lead$=125 \mathrm{J} {\mathrm{kg}}^{-1} {\mathrm{K}}^{-1}$.

$1 \mathrm{g}$ of ice at $0 °\mathrm{C}$ is mixed with $1 \mathrm{g}$ of steam at $100 °\mathrm{C}$. After thermal equilibrium is achieved, the temperature of the mixture is

The specific heat of metal at low temperatures varies according to $S=a{T}^3$ where $a$ is constant and $T$ is the absolute temperature. The heat energy needed to raise the unit mass of the metal from temperature $T=1 \mathrm{K}$ to $T=2 \mathrm{K}$ is

Three liquids $P$, $Q$ and $R$ are given $4 \mathrm{kg}$ of $P$ at $60 °\mathrm{C}$ and $1 \mathrm{kg}$ of $R$ at $50 °\mathrm{C}$ when mixed produce a resultant temperature $55 °\mathrm{C}$. A mixture of $1 \mathrm{kg}$ of $P$ at $60 °\mathrm{C}$ and $1 \mathrm{kg}$ of $Q$ at $50 °\mathrm{C}$ shows a temperature of $55 °\mathrm{C}$. What will be the resulting temperature when $1 \mathrm{kg}$ of $Q$ at $60 °\mathrm{C}$ is mixed with $1 \mathrm{kg}$ of $R$ at $50 °\mathrm{C}$?

$15 \mathrm{g}$ ice at $0 °\mathrm{C}$ is mixed with $10 \mathrm{g}$ water at $40 °\mathrm{C}$. Find the temperature of the mixture. Also, find the mass of water and ice in the mixture.

The temperature of $100 \mathrm{g}$ of water is to be raised from $24 °\mathrm{C}$ to $90 °\mathrm{C}$ by adding steam to it. Calculate the mass of the steam required for this purpose. [$s_{\mathrm{water}}=1 \mathrm{cal} {\mathrm{g}}^{-1} °{\mathrm{C}}^{-1}$,$L_{\mathrm{vapourization}}=540 \mathrm{cal} {\mathrm{g}}^{-1}$ ]

A lead bullet just melts when stopped by an obstacle. Assuming that $25 \%$ of the heat is absorbed by the obstacle, find the velocity of the bullet if its initial temperature is $27 °\mathrm{C}$. (Melting point of lead$=327 °\mathrm{C}$, specific heat of lead$=0.03 \mathrm{cal} {\mathrm{g}}^{-1} °{\mathrm{C}}^{-1}$, latent heat of fusion of lead$=6 \mathrm{cal} {\mathrm{g}}^{-1}$, $J=4.2 \mathrm{J} {\mathrm{cal}}^{-1}$).

Equal masses of ice (at $0 °\mathrm{C}$) and water are in contact. Find the temperature of water needed to just melt the complete ice.