Kirchhoff's Laws
Important Questions on Kirchhoff's Laws
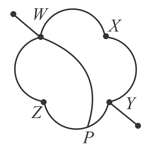
In the given mesh , each wire is uniform wire of resistance . If a wire of resistance is connected across $\mathrm{WP}$ and a constant potential difference is applied across , points and will be equipotential. Then point on placed such that
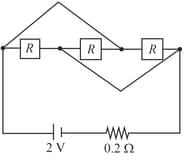
Three equal resistors, each is connected as shown in the figure. The value of for which heat generated in the circuit is maximum is
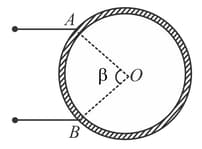
A wire of resistor is bent into a circular ring of radius . Equivalent resistance between two points and on its circumference, when angle is , can be given by
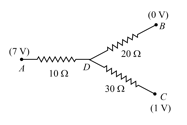
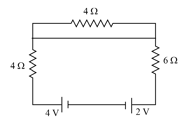
In the network shown in the figure, points , and are at potentials of , and respectively. Which of the following statements is INCORRECT?
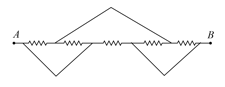
Resistors, each of value are arranged as shown in figure. The equivalent resistance between points and is
A battery of and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of resistors each of resistance .
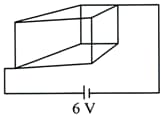
The current through the battery is
Assertion: A wire of uniform cross-section and uniform resistivity is connected across an ideal cell. Now the length of wire is doubled keeping volume of wire constant. The drift velocity of electrons after stretching the wire becomes one fourth of what it was before stretching the wire.
Reason: If a wire (of uniform resistivity and uniform cross-section) of length $l_{0}$ is stretched by a factor $n,$ then its resistance becomes $n^{2}$ times the one before stretching the wire (the volume of wire is kept constant in stretching process.) Further at constant potential difference, current is inversely proportional to resistance. Drift velocity of free electron is directly proportional to current and inversely proportional to cross-sectional area of current carrying wire.
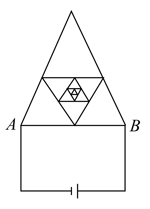
A frame is made of thin homogeneous wire (as shown in figure). Assuming that the number of successively embedded equilateral triangles (with sides decreasing by half) tends to infinity, where side is equal to and the resistance of unit length of the wire is the resistance between points and is
The current through the resistor shown in the figure is
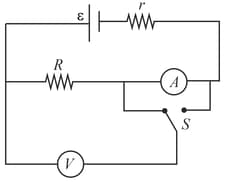
The e.m.f. and the internal resistance of the battery shown in figure are and respectively. The external resistance is . The resistance of the ammeter and voltmeter are and respectively. If the switch is thrown to the other side, the reading of the ammeter will be
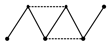
A certain wire is made up into two squares with a common side of length . A current enters the rectangular network at one of the corners and leaves at the diagonally opposite corner. The current in the common side in terms of the entering current is
A cell has an emf of and internal resistance . It is connected to an ammeter having resistance and to an external resistance of . When a voltmeter is connected across the resistance, the ammeter reading is . The resistance of the voltmeter is
Atul decides to use his bathtub water to generate electric power to run a bulb. The bathtub is located at a height of from the ground and has a capacity of . If he installs a water-driven wheel generator on the ground, at what rate in should the water drain from the bathtub to light the bulb? How long can we keep the bulb on if the bathtub was full initially? The efficiency of generator is
An ammeter and a voltmeter are connected in series to a cell. Their readings are and respectively. If a resistance is now joined in parallel with the voltmeter, then
Five identical resistors each of resistance are initially arranged as shown in the figure by dark lines. If two similar resistances are added as shown by the dashed lines, then change in resistance in final and initial arrangement is
A circuit consists of two cells, each of e.m.f. and internal resistances and are connected in series through an external resistance . If the potential difference between the ends of the first cell is zero, the value of in terms of and will be
A section of a circuit is shown in the figure. If electric levels at points respectively, then the potential at point is
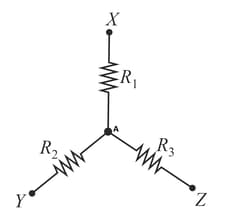
Figure (i) drawn below shows how four resistors are connected. A cell is connected between points and . If the cell has negligible internal resistance, the P.D. between points and is
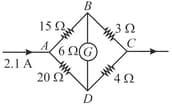
In the following network, the current flowing through $15 \Omega$ resistance is
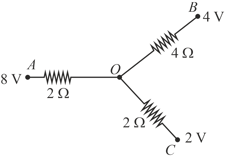
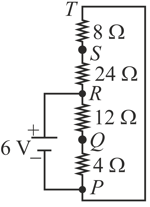
In the following network potential at $\mathrm{O}$ is