सरल लोलक के आवर्तकाल पर द्रव्यमान का प्रभाव

सरल लोलक और गोलक के द्रव्यमान क्या हैं?

सरल लोलक एक उपकरण है, जहां एक बिंदु द्रव्यमान एक हल्की अवितान्य डोरी से जुड़ा होता है और एक निश्चित आलम्ब से निलंबित होता है। एक सरल लोलक में माध्य स्थिति आमतौर पर वह बिंदु है, जहां से ऊर्ध्वाधर रेखा गुजरती है। जब लोलक अपनी औसत स्थिति में हो, तो लोलक की लंबाई (L) निलंबन बिंदु से पिंड के द्रव्यमान केंद्र तक ऊर्ध्वाधर दूरी है।

सरल शब्दों में, एक सरल लोलक एक यांत्रिक व्यवस्था है जो आवर्त गति को प्रदर्शित करती है। सरल लोलक में ‘m’ द्रव्यमान का एक छोटा-सा गोलक होता है, जो एक प्लेटफॉर्म से जुड़ी लंबाई L वाली एक पतली डोरी के ऊपरी सिरे से निलंबित होता है। यह दोलन गति करता है, जो गुरुत्वाकर्षण खिंचाव द्वारा संचालित होता है और ऊर्ध्वाधर तल में होता है।

सरल लोलक की गति से संबंधित कुछ महत्वपूर्ण पद:

• दोलनी गति – आवर्त गति में लोलक द्वारा की गई कोई भी आगे-पीछे की गति दोलनी गति होती है। जब लोलक अपनी केंद्रीय स्थिति में होता है, तो इस स्थिति को साम्यावस्था कहा जाता है।
• आवर्तकाल – यह आम तौर पर एक पूर्ण दोलन को पूरा करने के लिए लोलक द्वारा लिया गया कुल समय है; इसे ‘T’ से दर्शाया जाता है।
• आयाम – साम्यावस्था और लोलक की चरम स्थिति के बीच की दूरी।
• लंबाई – डोरी की लंबाई आम तौर पर डोरी के स्थिर सिरे से गोलक के द्रव्यमान केंद्र के बीच की दूरी होती है।

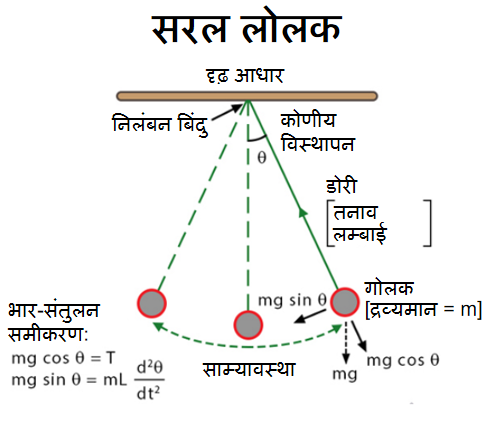
गोलक सहित सरल लोलक का आरेख

नीचे दिया गया चित्र एक सरल लोलक की गति के साथ-साथ किसी व्यापक कोणीय विस्थापन (θ) पर उस पर कार्य करने वाले बलों को दर्शाता है।

सरल लोलक के आवर्त पर द्रव्यमान का प्रभाव :

आइए सबसे पहले एक लोलक के आवर्तकाल की व्युत्पत्ति और उन कारकों को देखें जिन पर यह निर्भर करता है।

मान्यताएं:

1. यह एक घर्षण रहित परिवेश है।
2. लोलक की भुजाएँ कठोर एवं द्रव्यमान रहित हैं।
3. गुरुत्वीय त्वरण स्थिर है।
4. लोलक की गति एक सटीक तल में है।
   

एक छोटे कोणीय विस्थापन (θ) के लिए लोलक की गति:

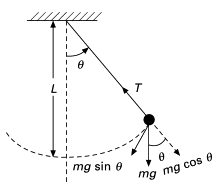
हम गति समीकरण का उपयोग कर सकते हैं:

${\displaystyle T–mg\cos \theta =m{v}^{2}L}$  (यहाँ T तनाव को और v स्पर्शरेखीय वेग को निरुपित करता है।)

यहां, आघूर्ण (τ) द्रव्यमान को साम्यावस्था स्थिति में लाता है:

${\displaystyle \tau =mgL\times \sin \theta =mg\sin \theta \times L=I\times \alpha }$

दोलन के छोटे कोणों के लिए, Sin θ ≈ θ

इसलिए, ${\displaystyle I\alpha =–mgL\theta }$(यहाँ – ve चिन्ह है, क्योंकि आघूर्ण θ कम हो रहा है))

${\displaystyle \alpha =–\frac{mgL\theta }{I}}$

${\displaystyle –{\omega }_0^2\theta =–\frac{mgL\theta }{I}}$  (यहाँ, ${\displaystyle {\omega }_0^{\mathrm{}}}$ लोलक की दोलनी गति की कोणीय आवृत्ति है।)

${\displaystyle {\omega }_0^2\theta =\frac{mgL}{I}}$

${\displaystyle {\omega }_0=\sqrt{\left(mg\frac{L}{I}\right)}}$

${\displaystyle I=M{L}^2}$ का उपयोग करते हुए,

यहाँ, I = गोलक का जड़त्व आघूर्ण 

${\displaystyle {\omega }_0=\sqrt{\left(\frac{g}{L}\right)}}$

इसलिए, सरल लोलक का आवर्तकाल (T) इस प्रकार दिया जाता है,

${\displaystyle T=\mathrm{}\frac{\mathrm{2\pi }}{{\omega }_0}=2\pi \times \sqrt{\left(\frac{L}{g}\right)}}$

तो, द्रव्यमान सहित सरल लोलक के आवर्तकाल के उपरोक्त व्यंजक से, हम देख सकते हैं कि एक सरल लोलक का आवर्तकाल डोरी की लंबाई और गुरुत्वीय त्वरण के मान पर निर्भर करता है। जैसा कि हम देख सकते हैं कि लोलक से जुड़ी वस्तु का द्रव्यमान सरल लोलक आवर्तकाल व्यंजक में नहीं है; इसलिए यह लोलक के द्रव्यमान से स्वतंत्र है।

इसलिए, गोलक का द्रव्यमान एक सरल लोलक के आवर्तकाल को प्रभावित नहीं करता है।

सरल लोलक के आवर्तकाल पर द्रव्यमान के प्रभाव का अध्ययन करने वाला प्रयोग

प्रयोग का शीर्षक – एक सरल लोलक के आवर्तकाल पर द्रव्यमान का प्रभाव

प्रयोग का विवरण – एक सरल लोलक आवर्त गति के सबसे सामान्य उदाहरणों में से एक है। इस प्रयोग में हम एक सरल लोलक के आवर्तकाल पर द्रव्यमान के प्रभाव का प्रेक्षण और अध्ययन करेंगे।

प्रयोग का उद्देश्य – किसी लोलक के द्रव्यमान के साथ उसके आवर्तकाल में परिवर्तन का अध्ययन करना।

आवश्यक उपकरण या सामग्री – एक स्टॉपवॉच, लोहे का एक भारी स्टैंड, एक कॉर्क (बीच से लंबाई में विभक्त), लगभग 1.5 m लंबाई का एक अवितान्य धागा, ज्ञात द्रव्यमान और व्यास के तीन अलग-अलग धातु के गोलाकार गोलक, एक बड़े आकार का चांदा, एक मापक पैमाना (200 cm)

कार्यविधि –

• स्टॉपवॉच का अल्पतमांक मापें।
• 1.5 मीटर की एक अवितान्य और हल्की डोरी लें और उसके एक सिरे को लोलक के गोलक से बांध दें।
• अब धागे के दूसरे सिरे को विभक्त कॉर्क से गुजारें, जैसा कि नीचे चित्र में दिखाया गया है।

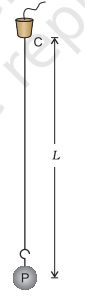
• कॉर्क को लोहे के एक भारी स्टैंड से मजबूती से क्लैंप करें और इसे एक क्षैतिज मेज पर इस तरह रखें कि लोलक मेज के ऊपर लटका रहे।
• लोलक की प्रभावी लंबाई को निलंबन बिंदु (विभक्त कॉर्क पर सबसे निचला बिंदु, जहां से गोलक स्वतंत्र रूप से निलंबित होता है) से लोलक के गोलक के द्रव्यमान केंद्र तक मापा जाता है, जो गोलाकार पिंड की स्थिति में इसके ज्यामितीय केंद्र पर होता है। क्लैंप की पकड़ को थोड़ा ढीला करने के बाद विभक्त कॉर्क के माध्यम से धागे को नीचे (या ऊपर) खींचकर लोलक की प्रभावी लंबाई L को 100 cm तक समायोजित करें। सरल लोलक की लंबाई नोट करें।
• विभक्त कॉर्क के ठीक नीचे एक बड़ा चांदा इस तरह लगाएं कि उसकी 0° – 180° रेखा क्षैतिज हो ताकि लंबवत लटका हुआ लोलक चांदे की 90° रेखा के साथ संपाती हो। यह भी सुनिश्चित करें कि चांदे का केंद्र लोलक के निलंबन बिंदु C के ठीक नीचे स्थित है, जैसा कि नीचे दिए गए चित्र में दिखाया गया है।

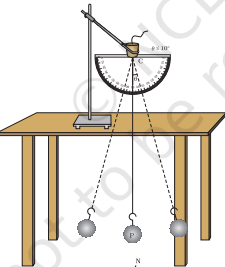
• सतह पर दो रेखाएँ एक मेज की भुजा (AB) के समानांतर और दूसरी उसके लंबवत (MN) खींचें, ताकि दोनों बिंदु O पर प्रतिच्छेद करें।
• लोहे के स्टैंड की स्थिति को इस प्रकार समायोजित करें कि लोलक का गोलक बिंदु O के ऊपर लंबवत स्थित हो।
• क्लैंप की ऊंचाई इस प्रकार समायोजित करें कि लोलक का गोलक बिंदु O के ठीक ऊपर रहे।
• लोलक के गोलक को पकड़ें और डोरी को खींचकर इसे 100 से अधिक के कोण पर बाएं या दाएं ले जाएं और छोड़ दें।
• स्टॉपवॉच की सहायता से लोलक द्वारा दस दोलनों को पूरा करने में लगने वाले समय का प्रेक्षण करें और इसे प्रेक्षण तालिका में रिकॉर्ड करें।
•  लोलक को उसकी माध्य स्थिति में विराम की स्थिति में लाएँ। उसी धात्विक गोलक के लिए चरण 10 और 11 दोहराएं और फिर लिया गया समय रिकॉर्ड करें।
• लोलक के गोलक को ज्ञात द्रव्यमान (m₂) और व्यास (d₂) के दूसरे धात्विक गोलक से बदल दें। चरण 5 में दी गई विधि का उपयोग करके, सरल लोलक की कुल लंबाई अर्थात L को तदनुसार समायोजित करें।
• n दोलनों को पूरा करने में लगने वाले कुल समय को रिकॉर्ड करने के लिए चरण 10, 11 और 12 को दोहराएं।
• तीसरे दिए गए धात्विक गोलक के लिए चरण 13 और 14 दोहराएँ।

सावधानियां-

• सरल लोलक के आवर्तकाल प्रयोग में उपयोग किया जाने वाली डोरी पतली, हल्की, मजबूत और अवितान्य होनी चाहिए। डोरी में तन्यता होने से लोलक की प्रभावी लंबाई बढ़ जाएगी। धागे में कोई मोड़ या मोड़ नहीं होना चाहिए।
• पूरे प्रयोग के दौरान सरल लोलक की कुल लंबाई समान रखी जानी चाहिए।
• प्रयोगशाला स्टैंड कठोर होना चाहिए।
• विभक्त कॉर्क को इसके निचले हिस्से को क्षैतिज रखते हुए क्लैंप किया जाना चाहिए।
• दोलन के दौरान, लोलक को मेज की भुजा या सतह को नहीं छूना चाहिए।
• लोलक के गोलक का इसकी माध्य स्थिति से विस्थापन कम होना चाहिए।
• गोलक को उसकी विस्थापित स्थिति से धीरे से और बिना किसी धक्के के छोड़ा जाना चाहिए; अन्यथा, यह सीधी रेखा AB के अनुदिश गति नहीं कर पाएगा। यदि आप देखते हैं कि दोलन दीर्घवृत्तीय हैं या गोलक घूम रहा है या ऊपर-नीचे कूद रहा है, तो लोलक को रोकें और इसे फिर से विस्थापित करें।
• प्रयोग के स्थान पर वायु का कोई व्यवधान नहीं होना चाहिए। प्रेक्षण दर्ज करते समय सभी पंखे बंद कर देने चाहिए।
• दोलनों की गिनती तब शुरू होनी चाहिए जब दोलनशील लोलक का गोलक अपनी माध्य स्थिति से गुजरता है।

सरल लोलक के आवर्तकाल पर द्रव्यमान के प्रभाव पर अक्सर पूछे जाने वाले प्रश्न