Growth and Decay of Current in a LR Circuit

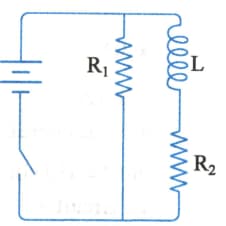
An inductor of inductance $\mathrm{L}=400 \mathrm{mH}$ and resistors of resistances  ${\mathrm{R}}_1=2 \mathrm{\Omega }$ and ${\mathrm{R}}_2=2 \mathrm{\Omega }$ are connected to a battery of $\mathrm{emf} 12 \mathrm{V}$ as shown in Fig. The internal resistance of the battery is negligible. The switch $\mathrm{S}$ is closed at $\mathrm{t}=0.$ The potential drop across $\mathrm{L}$ as a function of time is

A coil of inductance $8.4 \mathrm{mH}$ and resistance $6 \mathrm{\Omega }$ is connected to a $12 \mathrm{V}$ battery. The current in the coil is $1.0 \mathrm{A}$ at approximately the time 

A coil of inductance $300 \mathrm{mH}$ and resistance $2 \mathrm{\Omega }$ is connected to a source of voltage $2 \mathrm{V}$. The current reaches half of its steady state value in

An inductor of $2 \mathrm{H}$ and a resistance of $10 \mathrm{\Omega }$ are connected in series with a battery of $5 \mathrm{V}$. The initial rate of change of current is

An ideal coil of $10 \mathrm{H}$ is connected in series with a resistance of $5 \mathrm{\Omega }$ and a battery of $5 \mathrm{V}.2 \mathrm{s}$ after the connection is made, the current flowing (in ampere) in the circuit is

A parallel plate capacitor $\mathrm{C}$ with plates of unit area and separation $\mathrm{d}$ is filled with a liquid of dielectric constant $\mathrm{k}=2$ The level of liquid is $\frac{\mathrm{d}}{3}$ initially. Fig. Suppose the liquid level decreases at a constant speed $\mathrm{v}$, the time constant as a function of time is

What is mean by time-constant of a d.c. circuit with a resistor $R$ and an inductor $L$ connected in series.

In the $\mathrm{R}-L$ series circuit the resistance $R=30\Omega ,$ reactance $X_L=40\Omega$ and peak emf $E_0=220 \mathrm{V}.$ Calculate :

peak current $i_0$ in circuit.

What is mean by time-constant of a d.c. circuit with a resistor $R$ and an inductor $L$ connected in series.

Show that both during charging and discharging of a capacitor through a resistance, the current starts with its maximum value and falls off exponentially.

Establish the equation describing the decay of current in a $L-R$ circuit. Define the time constant for the circuit.

A steady current is flowing in an electric circuit containing an inductance $L$ and resistance $R$  in series. All of a sudden the battery is removed from the circuit without breaking the circuit. Explain how current decays smoothly.

An electric circuit has an inductance $L,$ a resistance $R$ connected in series with a battery of emf $\epsilon .$ Discuss how current grows in the circuit when circuit is switched on. Draw graph to show its variation.

Write the expression for frequency of an ideal $LC$ circuit. In an actual circuit, why do the oscillations ultimately die away ?

What are the factors on which the power factor depends?