Rolling Without Slipping

A circular disc rolls on a horizontal floor without slipping and the centre of disc moves with a uniform velocity $v$. Which of the following values the velocity at a point on the ring of the disc can have?

A block with length, breadth and height respectively as $a$, $a$ and $h$ is placed on a rough inclined plane. The inclination of plane is gradually increased. If $\mu$ is the coefficient of friction, the block will

A sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, $A$ is the point of contact, $B$ is the centre of the sphere and $C$ is the topmost point. Then

A hollow sphere and a solid sphere having the same mass and the same radius are rolled down a rough inclined plane.

Two uniform solid spheres having unequal masses and unequal radii are released from rest from the same height on a rough incline. If the spheres roll without slipping

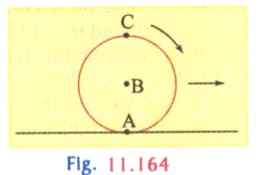
A wheel of radius $\mathrm{r}$ rolls without slipping with a speed $v$ on horizontal road. When it is at a point $A$ on the road, a small blob of mud separates from the wheel at its highest point and lands at point $B$ on the road.

A coin of radius $r$ rolls without slipping on a smooth horizontal plane. If the velocity of the centre of mass is $v$, then what is the velocity of point $A$ on the coin as shown in figure ?

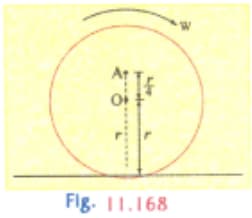
A uniform disc of radius $R$ is rolling (without slipping) on a horizontal surface with an angular speed $\omega$ as shown in figure (Fig. 11.167). $O$ is the centre of the disc, points $A$ and $C$ are located on its rim and $B$ is at distance $\frac{R}{2}$ from $O$. During rolling, the points $A, B$ and $C$ lie on the vertical diameter at a certain instant of time. If $v_A, v_B$ and $v_C$ are the linear speeds of points $A, B$ and $C$ respectively at that instant, then:

A cylinder rolls up an inclined plane, reaches some height, and then rolls down (without slipping throughout these motions). The directions of the frictional force acting on the cylinder are

A uniform rod $AB$ of mass $\mathrm{m}$ and length $L$ is suspended by two strings $C$ and $D$ of negligible mass as shown in the figure  When the string $D$ is cut, the tension in the string $C$ will be:

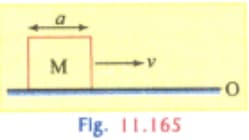
A cubical block of side$a$ is moving with a velocity $\mathrm{v}$ on a horizontal smooth plane as shown in the figure. It hits a ridge at the point $O$. The angular speed of the block after it hits the ridge at $O$ is:

A solid sphere of radius $10 \mathrm{cm}$ and mass $1 \mathrm{kg}$ rolls without slipping with uniform velocity of $100 \mathrm{cm}/\mathrm{s}$ along a straight line on a horizontal table. Calculate the total energy.

A solid cylinder is rolling down a rough inclined plane of inclination $\theta$. Then

A small object of uniform density rolls up a curved surface with an initial velocity $\mathrm{v}$  It reaches up to a maximum height of $\frac{3v^2}{4g}$ with respect to the initial position. The object is

A solid cylinder rolls without slipping on an inclined plane inclined at an angle $\theta$. Find the linear acceleration of the cylinder. Mass of the cylinder is $M$.

A rod of length $L$ and mass $M$ is hinged at a point $O$. A small bullet of mass $m$ hits the rod as shown in Fig. 11.152. The bullet gets embedded in the rod. Find angular velocity of the system just after impact.

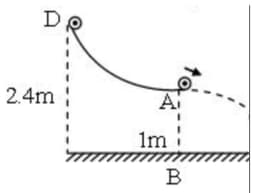
A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontal part is $1.0$ metre above the ground level and the top of the track is $2.4$ metre above the ground. Find the distance on the ground with respect to the point $B$ (which is vertically below the end of the track as shown in the figure, where the sphere lands. During its flight as a projectile, does the sphere continue to rotate about its centre of mass? Explain.

A carpet of mass $M$, made of inextensible, material is rolled along its length in the form of cylinder of radius $R$ and is kept on a rough floor. The carpet starts unrolling without sliding on the floor when a negligibly small push is given to it. Calculate the horizontal velocity of the axis of the cylindrical part of the carpet when its radius reduces to $\frac{R}{2}$.

A bullet of mass $10 \mathrm{g}$ and speed $500 \mathrm{m}/\mathrm{s}$ is fired into a door and gets embedded exactly. at centre of the door. The door is $1.0 \mathrm{m}$ wide and weighs $12 \mathrm{kg}$. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the impact.

How far above its centre should a billiard ball be struck in order to make it roll without any initial slipping. Radius of ball is $R$ and the impulse given is purely horizontal.