Academic Experts Solutions for Chapter: Moving Charges and Magnetism, Exercise 2: Force Acting on a Charged Particle in Magnetic Field

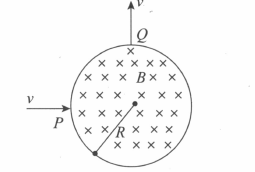
A particle of charge $q$ and mass $m$ enters normally (at point $P$) in a region of magnetic field with speed $v$. It comes out normally from $Q$ after time $T$ as shown in figure. The magnetic field $B$ is present only in the region of radius $R$ and is uniform as shown. Initial and final velocities are along radial direction and they are perpendicular to each other. For this to happen, which expression is correct?

A charged particle is released from rest in a region of uniform electric and magnetic fields, which are parallel to each other. The locus of the particle will be a 

The charges $1,2,3$ are moving in a uniform transverse magnetic field. Then 

A charged particle moves through a magnetic field perpendicular to its direction. Then 

A proton, a deuteron and an $\alpha$-particle having the same kinetic energy are moving in circular trajectories in a constant magnetic field. If $r_p, r_d$ and $r_{\alpha }$ denote, respectively, the radii of the trajectories of these particles, then

An electron is projected in vertically upward direction. If a uniform magnetic field acts from south to north, then it will be deflected

An $\alpha$-particle of $1 \mathrm{MeV}$ energy moves along a circular path in a uniform magnetic field. The kinetic energy of a proton in the same magnetic field for a circular path of double radius is

A proton is projected with a speed of  $2\times {10}^6 \mathrm{m} {\mathrm{s}}^{-1}$ at an angle ${60}^{\circ }$ towards the $x-\mathrm{axis}$. If a uniform magnetic field of  $0.1 \mathrm{T}$ is applied along the $y-\mathrm{axis}$, the path of the proton is