Projectile Motion on an Inclined Plane

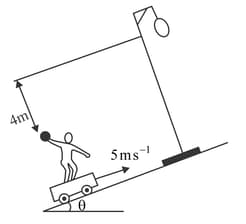
A man is travelling on a flat car which is moving up a plane inclined at $\cos \theta =\frac{4}{5}$ to the horizontal with a speed $5 \mathrm{m} {\mathrm{s}}^{-1}$. He throws a ball towards a stationary hoop located perpendicular to the incline in such a way that the ball moves parallel to the slope of the incline while going through the centre of the hoop. The centre of the hoop is $4 \mathrm{m}$ high from the man's hand calculate the time taken (in $\mathrm{s}$) by the ball to reach the hoop in second. 

Two parallel straight lines are inclined to the horizontal at an angle $\mathrm{\alpha }.$ A particle is projected from a point midway between them to graze one of the lines and strikes the other at right angles. Show that if $\mathrm{\theta }$ is the angle between the direction of projection and either of lines, then $\mathrm{tan\theta }=(\sqrt{2}-1)\mathrm{cot\alpha }$.

A stone is projected horizontally from a point $P$, so that it hits the inclined plane perpendicularly. The inclination of the plane with the horizontal is $\mathrm{\theta }$ and the point $P$ is at a height $h$ above the foot of the incline, as shown in the figure. Determine the velocity of the projection.

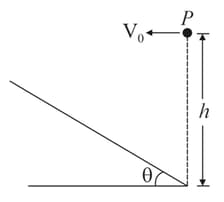
A projectile is fired at an angle $\theta$ with the horizontal. Find the condition under which it lands perpendicular on an inclined plane of inclination $\alpha$ as shown in the figure.

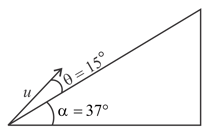
A plane is inclined at an angle $\mathrm{\alpha }=30°$ with respect to the horizontal. A particle is projected with a speed $u=2 \mathrm{m} {\mathrm{s}}^{-1}$ from the base of the plane making an angle $\mathrm{\theta }=15°$ with respect to the plane as shown in the figure. The distance from the base at which the particle hits the plane is close to:
(Take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$ )

Three stones $A, B, C$ are projected from the surface of a very long inclined plane with equal speeds and different angles of projection as shown in the figure. The incline makes an angle $\theta$ with horizontal. If $H_A, H_B$ and $H_C$ are maximum height attained by $A, B$ and $C$ respectively above inclined plane then: (Neglect air friction)

On an inclined plane of inclination $30°,$ a ball is thrown at an angle of $60°$ with the horizontal from the foot of the incline with a velocity of $10\sqrt{3} \mathrm{m} {\mathrm{s}}^{-1}$. If $g=10 \mathrm{m} {\mathrm{s}}^{-2}$, then the time in which the ball will hit the inclined plane is $30°$.

A particle is projected at angle $37°$ with the incline plane in upward direction with speed $10 \mathrm{m} {\mathrm{s}}^{-1}$. The angle of the inclined plane is given $53°$. Then the maximum distance from the inclined plane attained by the particle will be-

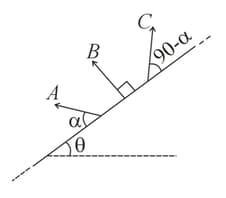
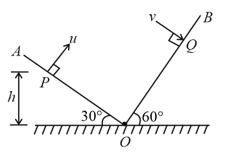
Two inclined planes $\mathrm{OA}$ and $\mathrm{OB}$, having inclinations (with the horizontal) of $30°$ and $60°$, respectively, intersect each other at $O$, as shown in the figure.

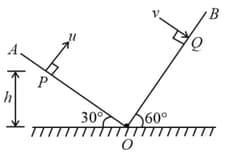
A particle is projected from point $P$ with velocity $\mathrm{u}=10\sqrt{3} \mathrm{m} {\mathrm{s}}^{-1}$ along a direction perpendicular to plane $\mathrm{OA}$. If the particle strikes plane $\mathrm{OB}$ perpendicularly at $Q$, the distance $PQ$ is:

The projected velocity is, $u=10\sqrt{3} \mathrm{m} {\mathrm{s}}^{-1}$, The height $h$ of point $P$ from the ground is:-

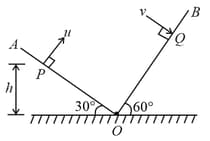
A ball is horizontally projected with a speed $v$ from the top of a plane inclined at an angle $45°$ with the horizontal. How far from the point of projection will the ball strike the plane?

Projected velocity is, $u=10\sqrt{3} \mathrm{m} {\mathrm{s}}^{-1}$, The speed with which the particle strikes the plane $OB$ is:-

A plane surface is inclined making an angle $\theta$ with the horizontal. From the bottom of this inclined plane, a bullet is fired with velocity $v$. The maximum possible range of the bullet on the inclined plane is

Projected velocity is, $u=10\sqrt{3} \mathrm{m} {\mathrm{s}}^{-1}$, The time of flight from $P$ to $Q$ is :-

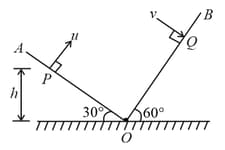
A particle is projected at an angle $\theta$ with an inclined plane making an angle $\beta$ with the horizontal as shown in the figure, speed of the particle is $u,$ after time$t$ find:

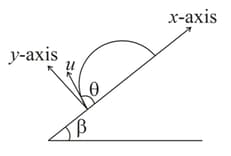
(a)$x$ component of acceleration?
(b) $y$ component of acceleration?
(c) $x$ component of velocity?
(d) $y$ component of velocity?
(e) $x$ component of displacement?
(f) $y$ component of displacement?
(g) $y$ component of velocity when the particle is at maximum distance from the inclined plane?