Magnetic Field Due to a Current Carrying Circular Coil

A circular coil of $100$ turns and having an effective radius of $0.05 \mathrm{m}$ carries a current of $0.1 \mathrm{A}$. How much work is required to turn it in an external magnetic field of $1.5 \mathrm{Wb} {\mathrm{m}}^{-2}$ through $180°$ about an axis perpendicular to the magnetic field. The plane of the coil is initially perpendicular to the magnetic field

A long insulated copper wire is closely wound as a spiral of$N$ turns. The spiral has inner radius $a$ and outer radius$b$. The spiral lies in the X-Y plane and a steady current I flows through the wire. The Z component of the magnetic field at the center of the spiral is

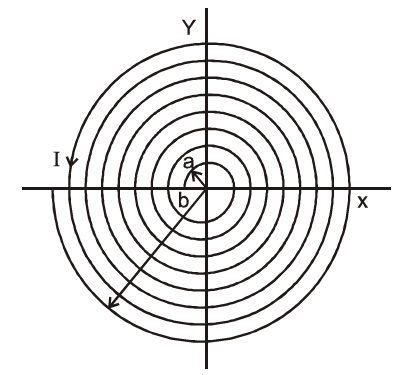
A circular loop of the radius $0.3 \mathrm{cm}$ lies parallel to a much bigger circular loop of radius $20 \mathrm{cm}.$ The centre of the small loop is on the axis of the bigger loop. The distance between their centres is$15 \mathrm{cm}.$If a current of $2.0 \mathrm{A}$ flows through the smaller loop, then the flux linked with bigger loop is:

Two identical wires $A$ and $B,$ each of length $l,$carry the same current $I.$ Wire $A$ is bent into a circle of radius $R$ and wire $B$ is bent to form a square of side $a$. If $B_A$ and $B_B$ are the values of magnetic field at the centres of the circle and square respectively, then the ratio $\frac{B_A}{B_B}$ is

The earth's magnetic field at a certain point is $7.0 \times {10}^{–5} \mathrm{T}$. This field is to be balanced by a magnetic field at the centre of a circular current carrying coil of radius $5.0 \mathrm{cm}$ by suitably orienting it. If the coil has $100$ turns then the required current is about

A ring of mass $m$ and radius $r$ is rotated in uniform magnetic field $B$ which is perpendicular to the plane of the loop with constant angular velocity ${\omega }_0$. Find the net ampere force on the ring and the tension developed in the ring if there is a current i in the ring. Current and rotation both are clockwise.

A circular coil of radius $20 \mathrm{cm}$ and $20$ turns of wire is mounted vertically with its plane in magnetic meridian. A small magnetic needle (free to rotate about vertical axis) is placed at the center of the coil. It is deflected through $45°$ when a current is passed through the coil and in equilibrium (Horizontal component of earth's field is $0.34 \times {10}^{–4} \mathrm{T}$). The current in coil is

A circular loop is kept in that vertical plane which contains the north-south direction. It carries a current that is towards south at the topmost point. Let $\mathrm{A}$ be a point on axis of the circle to the east of it and $\mathrm{B}$ a point on this axis to the west of it. The magnetic field due to the loop

A circular loop of radius $\mathrm{r}$ carries a current $\mathrm{i}$. How should a long, straight wire carrying a current $3\mathrm{i}$ be placed in the plane of the circle so that the magnetic field at the centre of the loop becomes zero?

A battery is connected between two points $\mathrm{A}$ and $\mathrm{B}$ the circumference of a uniform conducting ring of radius $r$ and resistance $R$. One of the arcs $\mathrm{AB}$ of the ring subtends an angle $\mathrm{\theta }$ at the centre. The value of the magnetic induction at the centre due to the current in the ring is:

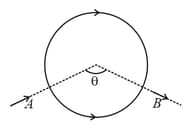
 A current carrying wire $\mathrm{AB}$ of the length $2\pi R$ is turned along a circle, as shown in figure. The magnetic field at the centre $O$.

A long cylinder of radius a carrying a uniform surface charge rotates about its axis with an angular velocity $\mathrm{\omega }$. Find the magnetic field energy per unit length of the cylinder if the linear charge density equals $\mathrm{\lambda } \mathrm{and} \mathrm{\mu r} = 1.$

A coil $\mathrm{ACD}$of $\mathrm{N}$ turns & radius $\mathrm{R}$ carries a current of $\mathrm{I} \mathrm{Amp}$& is placed on a horizontal table. $\mathrm{K}$ is a very small horizontal conducting ring of radius $\mathrm{r}$ placed at a distance $\mathrm{Y}$ from the centre of the coil vertically above the coil $\mathrm{ACD}.$ Find an expression for the $\mathrm{EMF}$established when the ring $\mathrm{K}$ is allowed to fall freely. Express the $\mathrm{EMF}$ in terms of instantaneous speed $\mathrm{v}$& height $\mathrm{Y}.$

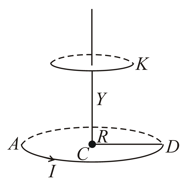
Find the magnetic induction at the point $O$ if the wire carrying a current $I$ has the shape shown in figure $a, b, c$. The radius of the curved part of the wire is $R$, the linear parts of the wire are very long.

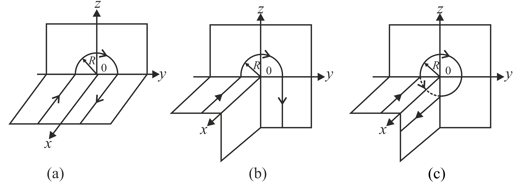
Find the magnetic induction of the field at the point $O$ of a loop with current $I$, whose shape is illustrated in figure

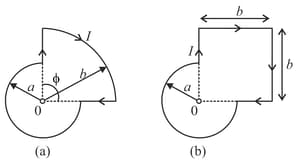
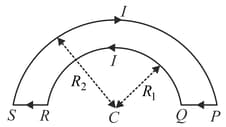
 (a) In figure $a$, the radii $a$ and $b$ as well as the angle $\varphi$ are known,

(b) In figure $b$, the radius $a$ and the side $b$ are known.

(c) A current $I=5.0 \mathrm{A}$ flows along a thin wire shaped as shown in the figure. The radius of a curved part of the wire is equal to $R=120 \mathrm{mm},$ the angle $2\varphi =90°$. Find the magnetic induction of the field at the point $O$.

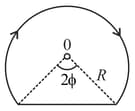
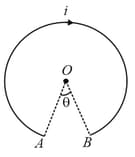
Find the magnitude of the magnetic induction $B$ of a magnetic field generated by a system of thin conductors (along which a current $i$ is flowing) at a point $\mathrm{A} (0, \mathrm{R}, 0)$, that is the centre of a circular conductor of radius $R$. The circular part is in $yz$ plane.

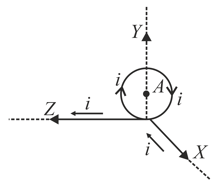
Two wire loops $\mathrm{PQRSP}$ formed by joining two semicircular wires of radii $R_1$ and $R_2$ carries a current $I$ as shown in (figure). The magnitude of the magnetic induction at the center $\mathrm{C}$ is 

(i) Two circular coils of radii $5.0 \mathrm{cm}$ and $10 \mathrm{cm}$ carry equal currents of $1 \mathrm{A}$. The coils have $50$ and $100$ turns respectively and are placed in such a way that their planes, as well as the centre, coincide. Find the magnitude of the magnetic field $B$ at the common center when the currents in the coils are (a) in the same sense (b) in the opposite sense. (ii) If the outer coil of the above problem is rotated through $90°$ about a diameter, what would be the magnitude of the magnetic field $B$ at the centre?

A particle of negative charge of magnitude $q$ is revolving with constant speed $V$ in a circle of radius $R$ as shown in the figure. Find the magnetic field (magnitude and direction) at the following points:

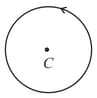
(i) centre of the circle (magnitude and direction)

(ii) a point on the axis and at a distance $x$ from the centre of the ring (magnitude only). Is its direction constant all the time?