Thermodynamic Processes and Indicator Diagrams

Find the work done in the process is, $5.6 \mathrm{L}$ of helium at $\mathrm{STP}$ is adiabatically compressed to $0.7 \mathrm{L}$. Taking the initial temperature to be $T_1$
 

Two rigid boxes containing different ideal gases are placed on a table. The boxes are then put into thermal contact with each other, and heat flows between them until the gases reach a common final temperature (ignore the heat capacity of boxes). Box A contains one mole of nitrogen at temperature $T_0$, while box $B$ contains one mole of helium at temperature $\frac{7}{3}{\mathit{ }\mathit{T}}_0$. Then the final temperature of the gases, $T_{\mathit{f}}$ in terms of $T_0$ is

A gas is enclosed in a cylinder with a movable frictionless piston. Its initial thermodynamic state at pressure $p_i={10}^5 \mathrm{Pa}$ and volume $V_i={10}^{-3} {\mathrm{m}}^3$ changes to a final state at $p_f=\left(\frac{1}{32}\right)\times {10}^5 \mathrm{Pa}$ and $V_f=8\times {10}^{-3} {\mathrm{m}}^3$ in an adiabatic quasi-static process, such that $p^3{V}^5=$constant. Consider another thermodynamic process that brings the system from the same initial state to the same final state in two steps: an isobaric expansion at $p_i$ followed by an isochoric (isovolumetric) process at volume $V_f$. The amount of heat supplied to the system in the two-step process is approximate,

During an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio $\frac{C_{\mathrm{p}}}{C_{\mathrm{V}}}$ for the gas is

When an ideal gas is compressed isothermally, then its pressure increases because

Cloud formation condition

Consider a simplified model of cloud formation. Hot air in contact with the earth’s surface contains water vapour. This air rises connectively till the water vapour content reaches its saturation pressure. When this happens, the water vapour starts condensing and droplets are formed. We shall estimate the height at which this happens. We assume that the atmosphere consists of the diatomic gases oxygen and nitrogen in the mass proportion $21:79$ respectively. We further assume that the atmosphere is an ideal gas, $g$ the acceleration due to gravity is constant and air processes are adiabatic. Under these assumptions one can show that the pressure is given by

$p=p_0{\left(\frac{T_0-\tau Z}{T_0}\right)}^{\alpha }$

Here $p_0$ and $T_0$ is the pressure and temperature respectively at sea level $(\mathrm{z} = 0), \tau$ is the lapse rate (magnitude of the change in temperature $T$ with height $z$ above the earth’s surface, i.e. $\tau > 0$).

(a) Obtain an expression for the lapse rate $\mathrm{\Gamma }$ in terms of $\gamma , R, g$ and $m_a$. Here $\mathrm{\gamma }$ is the ratio of specific heat at constant pressure to specific heat at constant volume; $R$, the gas constant; and $m_a$, the relevant molar mass. 

(b) Estimate the change in temperature when we ascend a height of one kilometre ?

(c) Show that pressure will depend on height as given by Eq. (1). Find an explicit expression for exponent $\mathrm{\alpha }$ in terms of $\mathrm{\gamma }$.

(d) According to this model what is the height to which the atmosphere extends? Take $T_0 = 300 \mathrm{K}$and $p_0 = 1 \mathrm{atm}.$

A Carnot engine cycle is shown in the figure (2). The cycle runs between temperatures$T_H=\alpha T_0 \text{and }{T}_L=T_0 (\alpha > 1).$ Minimum and maximum volume at state $1$ and state $3$ are ${\mathrm{V}}_0$ and $n{V}_0$, respectively. The cycle uses one mole of an ideal gas with $\frac{{\mathit{C}}_{\mathit{P}}\mathit{ }}{{\mathit{C}}_{\mathit{V}}}=\mathrm{\gamma }$. Here $C_P$and $C_V$ are the specific heats at constant pressure and volume respectively. You must express all answers in terms of the given parameters  $\left\{\alpha ,n,T_0,V_0\right\},?$ and universal gas constant $R$.

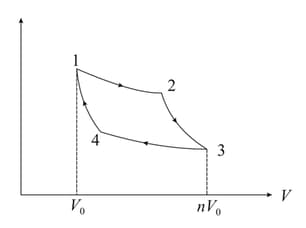
(a) Find $P, V, T$ for all the states

(b) Calculate the work done by the engine in each process $W_{12}, W_{23}, W_{34}, W_{41}.$

(c) Calculate $Q$, the heat absorbed in the cycle.

Two samples $A$ and $B$ of the same gas have equal volumes and pressures. The gas in sample $A$ is expanded isothermally to four times of its initial volume and the gas in $B$ is expanded adiabatically to double of its volume. If works done in isothermal process is twice that of adiabatic process, then show that $\gamma$ satisfies the equation $1 – 2^{\left(1–\gamma \right)}=(\mathrm{\gamma }–1)\mathrm{In}2.$

An ideal gas $\left(\frac{C_p}{C_v}=\gamma \right)$ having initial pressure $P_0$ and volume $V_0$.

(a) The gas is taken isothermally to a pressure $2P_0$ and then adiabatically to a pressure $4P_0$. Find the final volume.

(b) The gas is brought back to its initial state. It is adiabatically taken to a pressure $2P_{0 }$and then isothermally to a pressure $4P_0$. Find the final volume.

Two containers $A$ and $B$ of equal volume $\frac{V_0}{2}$ each are connected by a narrow tube which can be closed by a valve. The containers are fitted with pistons which can be moved to change the volumes. Initially, the valve is open and the containers contain an ideal gas $\left(\frac{C_p}{C_v}=\gamma \right)$ at atmospheric pressure $P_0$ and atmospheric temperature $2T_0$. The walls of the containers $A$ are highly conducting and of $B$ are non-conducting. The valve is now closed and the pistons are slowly pulled out to increase the volumes of the containers to double the original value. (a) Calculate the temperatures and pressures in the two containers. (b) The valve is now opened for sufficient time so that the gases acquire a common temperature and pressure. Find the new values of the temperature and the pressure.

A weightless piston divides a thermally insulated cylinder into two parts of volumes $\mathrm{V}$ and $3\mathrm{V}.2 \mathrm{moles}$ of an ideal gas at pressure $\mathrm{P} = 2$atmosphere are confined to the part with volume $\mathrm{V} = 1 \mathrm{liter}$. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, $\gamma =1.5.$

Two moles of a monatomic gas, initially at pressure $P_1$ and volume $V_1$, undergo an adiabatic compression until its volume becomes $V_2$. Then the gas is given heat $Q$ at constant volume $V_2$.

(a) Sketch the complete process on a $P-V$ diagram.

(b) Find the total work done by the gas, the total change in its internal energy and the final temperature of the gas.

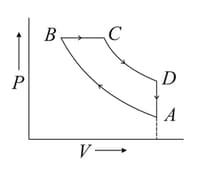
One mole of a diatomic ideal gas $(\mathrm{\gamma } = 1.4)$ is taken through a cyclic process starting from point $\mathrm{A}$. The process $\mathrm{A} \to \mathrm{B}$is an adiabatic compression. $\mathrm{B} \to \mathrm{C}$ is isobaric expansion. $\mathrm{C} \to \mathrm{D}$ an adiabatic expansion and $\mathrm{D} \to \mathrm{A}$ is isochoric as shown in P-V diagram. The volume ratios are $\frac{{\mathrm{V}}_{\mathrm{A}}}{{\mathrm{V}}_{\mathrm{B}}}=16 \& \frac{{\mathrm{V}}_{\mathrm{C}}}{{\mathrm{V}}_{\mathrm{B}}}=2$ and the temperature at $\mathrm{A}$ is ${\mathrm{T}}_{\mathrm{A}} = 300 \mathrm{K}$. Calculate the temperature of the gas at the points $\mathrm{B}$ and $\mathrm{D}$ and find the efficiency of the cycle.

At $27º \mathrm{C}$ two moles of an ideal monoatomic gas occupy a volume $\mathrm{V}$. The gas expands adiabatically to a volume $2\mathrm{V}$. Calculate:

(i) the final temperature of the gas,

(ii) change in its internal energy and 

(iii) the work done by the gas during the process.

A vessel of volume $V$ is evacuated by means of a piston air pump. In one stroke the piston is pulled out to make the volume of gas $V+∆V$ then $∆V$ volume from this is taken out leaving volume $V$ in the cylinder. How many strokes are needed to reduce the pressure in the vessel to $\frac{1}{\mathrm{\eta }}$ times the initial pressure? The process is assumed to be isothermal, and the gas is an ideal.

Consider a spherical shell of radius $R$ at temperature $T$. The black body radiation inside it can be considered as an ideal gas of photons with internal energy per unit volume $u=\frac{U}{V}\propto T^4$ and pressure $P=\frac{1}{3}\left(\frac{U}{V}\right)$. If the shell now undergoes an adiabatic expansion the relation between $T$ and $R$ is

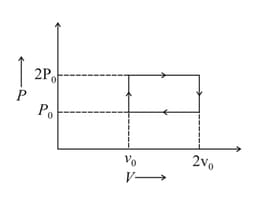
The above p-v diagram represents the thermodynamic cycle of an engine, operating with an ideal mono atomic gas. The amount of heat, extracted from the source in a single cycle is 

One mole of a monatomic ideal gas undergoes an adiabatic expansion in which its volume becomes eight times its initial value. If the initial temperature of the gas is $100 \mathrm{K}$ and the universal gas constant$8.0\mathrm{J} {\mathrm{mol}}^{–1}{\mathrm{K}}^{–1}$ , the decrease in its internal energy, in Joule, is__________.

A diatomic ideal gas is compressed adiabatically to $\frac{1}{32}$ of its initial volume. If the initial temperature of the gas is ${\mathrm{T}}_{\mathrm{i}}$ (in Kelvin) and the final temperature is a${\mathrm{T}}_{\mathrm{i}}$, the value of a is :

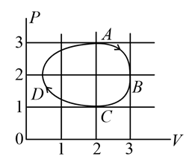
The figure shows the $P-V$ plot of an ideal gas taken through a cycle $\mathrm{ABCDA}$. The part $\mathrm{ABC}$ is a semi-circle and$\mathrm{CDA}$ is half of an ellipse. Then,