Embibe Experts Solutions for Chapter: Elasticity, Exercise 2: Exercise - 2

The compressibility of water is $46.4 \times {10}^{–6} {\mathrm{atm}}^{-1}$. This means that

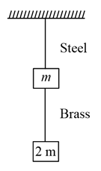
If the ratio of lengths, radii and Young’s moduli of steel and brass wires in the figure are $a, b$ and $c$ respectively. Then the corresponding ratio of increase in their lengths would be:

If a rubber ball is taken at the depth of $200 \text{m}$ in a pool, its volume decreases by $0.1\%$. If the density of the water is $1\times {10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$ and $g=10 \mathrm{m} {\mathrm{s}}^{-2}$, then the volume elasticity in $\mathrm{N} {\mathrm{m}}^{-2}$ will be

A rod $1 \mathrm{m}$ long is $10 {\mathrm{cm}}^2$ in the area for a portion of its length and $5 {\mathrm{cm}}^2$ in the area for the remaining. The strain energy of this stepped bar is $40 \%$ of that a bar $10 {\mathrm{cm}}^2$ in the area and $1 \mathrm{m}$ long under the same maximum stress. What is the length of the portion $10 {\mathrm{cm}}^2$ in area?

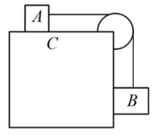
Two block $A$ and $B$ are connected to each other by a string, passing over a frictionless pulley as shown in the figure. Block $A$ slides over the horizontal top surface of a stationary block $C$ and block $B$ slide along the vertical side of $C$ both with uniform speed. The coefficient of friction between the surface of blocks is $0.2$. String stiffness is $2000 \mathrm{N} {\mathrm{m}}^{-1}$. If mass of block $B$ is $2 \mathrm{kg}$. Calculate ratio (in $\mathrm{kg} {\mathrm{J}}^{-1}$) of the mass of block $A$ and the energy stored in the string.

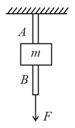
The wires $A$ and $B$ shown in the figure, are made of the same material and have radii $r_{\mathit{A}}$ and $r_{\mathit{B}}$. A block of mass $m \mathrm{kg}$ is tied between them. If the force $F$ is $\frac{mg}{3}$, one of the wires breaks.

A metal wire of length $L,$area of cross-section $A$ and young's modulus $Y$ is stretched by a variable force $F$ such that $F$ is always slightly greater than the elastic forces of resistance in the wire. When the elongation of the wire is $l$

Two plates of the same mass are attached rigidly to the two ends of a spring as shown in the figure. One of the plates rests on a horizontal surface and the other results a compression $y$ of the spring when it is in an equilibrium state. The further minimum compression required, so that after the force causing compression is removed the lower plate is lifted off the surface, will be,