D. C. Pandey Solutions for Chapter: Gravitation, Exercise 2: Excercise 2

Planet $A$ has mass $M$ and radius $R$. Planet $B$ has half the mass and half the radius of planet $A$. If the escape velocities from the planets $A$ and $B$ are $v_{\mathrm{A}}$ and $v_{\mathrm{B}}$ respectively, then $\frac{v_{\mathrm{A}}}{v_{\mathrm{B}}}=\frac{n}{4}$. The value of $n$ is

A body $A$ of mass $m$ is moving in a circular orbit of radius $R$ about a planet. Another body $B$ of mass $\frac{m}{2}$ collides with $A$ with a velocity which is half $\left(\frac{v}{2}\right)$, the instantaneous velocity $v$ of $A$. The collision is completely inelastic. Then, the combined body

A straight rod of length $L$ extends from $x=a$ to $x=L+a$. The gravitational force it exerts on a point mass $m$ at $x=0$, if the mass per unit length of the rod is $A+B{x}^2$, is given by

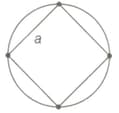
Four identical particles of mass $M$ are located at the corners of a square of side $a$. What should be their speed, if each of them revolves under the influence of other's gravitational field in a circular orbit circumscribing the square?

Two bodies each of mass $m$ are hung from a balance whose scale pans differ in a vertical height by $h$. If the mean density of the earth is $\rho$, the error in weighing is,

Two bodies of masses $m_1$ and $m_2$ initially at rest at infinite distance apart move towards each other under gravitational force of attraction. Their relative velocity of approach when they are separated by a distance $r$ is, ($G=$ universal gravitational constant.)

A hole is drilled halfway to the centre of the earth. A body weighs $300 \mathrm{N}$ on the surface of the earth. How much will it weigh at the bottom of the hole?