Embibe Experts Solutions for Chapter: Kinetic Theory of Gases, Exercise 3: Exercise-3

One mole of an ideal gas goes from an initial state $A$ to final state $B$ via two processes. It first undergoes isothermal expansion from volume $V$ to $3 V$ and then its volume is reduced from $3 V$ to $V$ at constant pressure. The correct $PV$ diagram representing the two processes is: 

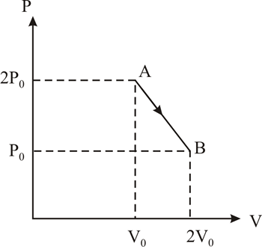
In the given $(V-T)$ diagram, what is the relation between pressure $P_1$ and $P_2$?

One $\mathrm{kg}$ of a diatomic gas is at pressure of $8\times {10}^4 \mathrm{N} {\mathrm{m}}^{-2}$. The density of the gas is $4 \mathrm{kg} {\mathrm{m}}^{-3}$. What is the energy of the gas due to thermal motions?

A container with insulating walls is divided into two equal parts by a partition fitted with a valve. One part is filled with an ideal gas at a pressure $p$ and temperature $T$, whereas the other part is completely evacuated. If the valve is suddenly opened, the pressure and temperature of the gas will be

$n$ moles of an ideal gas undergoes a process $A\to B$ as shown in the figure. The maximum temperature of the gas during the process will be:

An ideal gas is enclosed in a cylinder at pressure of $2 \mathrm{atm}$ and temperature, $300 \mathrm{K}$. Then mean time between two successive collisions is $6\times {10}^{-8} \mathrm{s}$. If the pressure is doubled and temperature is increased to $500 \mathrm{K}$, the mean time between two successive collisions will be close to

A vertical closed cylinder is separated into two parts by a frictionless piston of mass $m$ and of negligible thickness. The piston is free to move along the length of the cylinder. The length of the cylinder above the piston is $l_1$ and that below the piston is $l_2,$ such that $l_1>l_2$. Each part of the cylinder contains $n$ moles of an ideal gas at equal temperature $T$. If the piston is stationary, its mass, $m$, will be given by ( $R$ is the universal gas constant and $g$ is the acceleration due to gravity)

A flask containing air at $27 °\mathrm{C}$ is corked up at atmospheric pressure. The cork can be forced out by the pressure of $2.5$ atmosphere. To what temperature the flask should be heated to do that?