Embibe Experts Solutions for Chapter: Wave Motion on a String, Exercise 2: Exercise-2

Two stretched wires $A$ and $B$ of the same lengths vibrate independently. $1$ If the radius, density and tension of wire $A$ are respectively twice those of wire $B$, then the fundamental frequency of vibration of $A$ relative to that of $B$ is

The equation of a wave is represented by $y={10}^{-4}\sin \left(100t-\frac{\mathrm{\pi }x}{10}\right) \mathrm{m}$, where $x$ and $y$ are in $\mathrm{meter}$ and $t$ in $\mathrm{second}$, then the velocity of the wave will be

Vibrations of rope tied by two rigid ends are shown by the equation $y=\cos 2\mathrm{\pi }t\sin 2\mathrm{\pi }x$, then the minimum length of the rope will be

Two waves of intensities ratio are $9:1$, then the ratio of their resultant's maximum and minimum intensities will be

A metal wire of linear mass density of $9.8 \mathrm{g} {\mathrm{m}}^{-1}$ is stretched with a tension of $10 \mathrm{kg}$ wt between two rigid supports $1 \mathrm{metre}$ apart. The wire passes at its middle point between the poles of a permanent magnet, and it vibrates in resonance when carrying an alternating current of frequency $n$. The frequency $n$ of the alternating source is

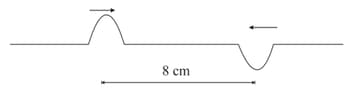
Two symmetrical and identical pulses in a stretched string, whose centres are initially $8 \mathrm{cm}$ apart, are moving towards each other as shown in the figure. The speed of each pulse is $2 \mathrm{cm} {\mathrm{s}}^{-1}$. After $2 \mathrm{seconds}$, the total energy of the pulses will be

Assertion : Standing waves do not transfered energy in the medium.

Reason : Every particle vibrates with its own energy and it does not share its energy with any other particle

Assertion : A wave can be represented by function $y=f(kx\pm \omega t).$ 

Reason : Because it satisfies the differential equation
$\frac{{\partial }^2\mathrm{y}}{\partial {\mathrm{x}}^2}=\frac{1}{{\mathrm{v}}^2}\left(\frac{{\partial }^2\mathrm{y}}{\partial {\mathrm{t}}^2}\right)\text{ where }\mathrm{v}=\frac{\omega }{\mathrm{k}}$