Assam Board Solutions for Chapter: Some Applications of Trigonometry, Exercise 1: Exercise 9.1
Assam Board Mathematics Solutions for Exercise - Assam Board Solutions for Chapter: Some Applications of Trigonometry, Exercise 1: Exercise 9.1
Attempt the practice questions on Chapter 9: Some Applications of Trigonometry, Exercise 1: Exercise 9.1 with hints and solutions to strengthen your understanding. MATHEMATICS Textbook for Class X solutions are prepared by Experienced Embibe Experts.
Questions from Assam Board Solutions for Chapter: Some Applications of Trigonometry, Exercise 1: Exercise 9.1 with Hints & Solutions
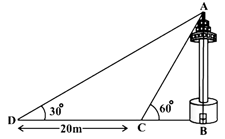
The angle of elevation of the top of a building from the foot of the tower is and the angle of elevation of the top of the tower from the foot of the building is . If the tower is high, find the height of the building.
Two poles of equal heights are standing opposite each other on either side of the road, which is wide. From a point between them on the road, the angles of elevation of the top of the poles are and , respectively. Find the height of the poles and the distances of the point from the poles.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is . From another point away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is . Find the height of the tower and the width of the canal.
From the top of a high building, the angle of elevation of the top of a cable tower is and the angle of depression of its foot is . Determine the height of the tower.
As observed from the top of a high lighthouse from the sea-level, the angles of depression of two ships are and . If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
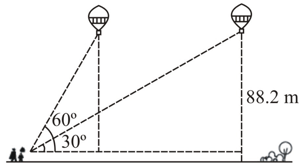
A tall girl spots a balloon moving with the wind in a horizontal line at a height of from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is . After some time, the angle of elevation reduces to (see Fig.). Find the distance travelled by the balloon during the interval.
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of , which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be .
Find the time taken by the car to reach the foot of the tower from this point.
The angles of elevation of the top of a tower from two points at a distance of and from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is .
