B M Sharma Solutions for Chapter: Coulomb's Laws and Electric Field, Exercise 4: DPP

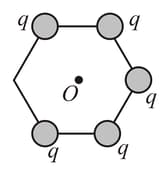
Five point charges each having magnitude $q$ are placed at the corner of hexagon, as shown in the figure. Net electric field at the centre $O$ is $\overrightarrow{E}$. To get the net electric field at $O$ as $6\overrightarrow{E},$the charge placed on the remaining sixth corner should be

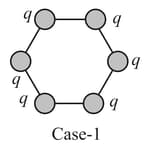
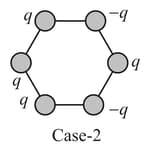
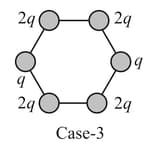
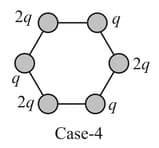
The following figures show regular hexagons, with charges at the vertices. In which of the following cases the electric field at the center is not zero?

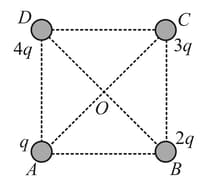
Charges $q, 2q, 3q$and $4q$are placed at the corners $A, B, C$and $D$of a square $ABCD$as shown in the following figure. The direction of the electric field at the center of the square is along

Infinite charges of magnitude $q$each are lying at $x=1, 2, 4, 8, ... \mathrm{m}$on the $x$ axis. The value of intensity of electric field at point $x=0$due to these charges will be

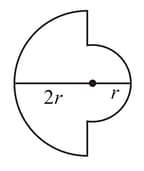
Two semicircular rings lying in the same plane of uniform linear charge density $\lambda$, have radii $r$and $2r.$They are joined using two straight uniformly charged wires of linear charge density $\lambda$and length $r$as shown in the figure. The magnitude of the electric field at the common centre of semicircular rings is

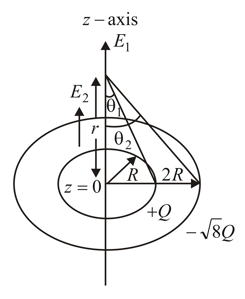
Two concentric rings, one of radius $R$and total charge $+Q$and the second of radius $2R$and total charge $-\sqrt{8}Q,$lie in the $xy$plane ($z=0$plane). The common center of rings lies at origin and the common axis coincides with the $z$ axis. The charge is uniformly distributed on both rings. At what distance from the origin is the net electric field on the $z$-axis zero?

An infinitely long wire is kept along $z$-axis from $z=-\infty$to $z=+\infty ,$having uniform linear charge density $\frac{10}{9} \mathrm{nC}/\mathrm{m}.$The electric field at the point $(6 \mathrm{cm},8 \mathrm{cm},10 \mathrm{cm})$will be

Two point charges $q_A$ and $q_B$ are placed at some separation on positive $x$-axis at points $\left(x_A, 0\right)$ and $\left(x_B, 0\right)$. It is given that $\left|q_A\right|>\left|q_B\right|$ and $x_B>x_A$. If the null point is the point where the net electric field due to both the charges is zero, then