B M Sharma Solutions for Chapter: Electric Current and Circuits, Exercise 2: DPP

Length of a hollow tube is $5 \mathrm{m}$. Its outer diameter is $10 \mathrm{cm}$ and thickness of its wall is $5 \mathrm{mm}$. If the resistivity of the material of the tube is $1.7\times {10}^{-8} \mathrm{\Omega } \mathrm{m}$ then the resistance of tube will be

In order to quadruple the resistance of a uniform wire, a part of its length was uniformly stretched till the final length of the entire wire was $1.5$ times the original length, the part of the wire was fraction equal to

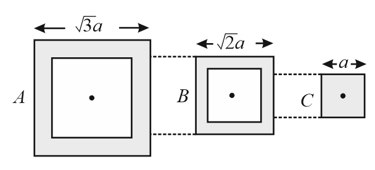
The following figure shows cross-sections through three long conductors of the same length and material, with a square cross-section of edge lengths as shown. Conductor $B$ will fit snugly within conductor $A$, and conductor $C$ will fit snugly within conductor $B$. Relationship between their end to end resistance is

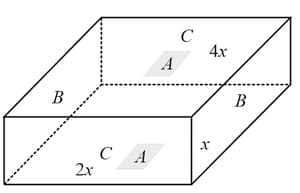
The following figure shows a rectangular block with dimensions $x$, $2x$ and $4x$. Electrical contacts can be made to the block between opposite pairs of faces (for example, between the faces labelled $A-A$, $B-B$ and $C-C$ ). Between which two faces would the maximum electrical resistance be obtained ($A-A$: Top and bottom faces, $B-B$: Left and right faces and $C-C$: Front and rear faces).

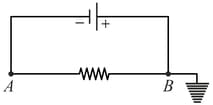
A battery is connected to a uniform resistance wire $AB$ and $B$ is earthed. Which one of the graphs below shows how the current density $J$ varies along $AB$?

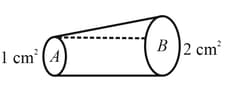
Two wires each of radius of cross-section $r$ but of different materials are connected together end to end (i.e., in series). If the densities of charge carriers in the two wires are in the ratio $1:4$, the drift velocity of electrons in the two wires will be in the ratio

A solid conductor has a cross-section area $1 {\mathrm{cm}}^2$ and $2 {\mathrm{cm}}^2$, as shown in the figure. A current of $20 \mathrm{A}$ enters at $A$. Then

A $150 \mathrm{m}$ long metal wire connects points $A$ and $B$. The electric potential at point $B$ is $50 \mathrm{V}$ less than that at point $A$. If the conductivity of the metal is $60\times {10}^6 \mathrm{mho} {\mathrm{m}}^{-1}$, then the magnitude of the current density in the wire is equal to: