B M Sharma Solutions for Chapter: Sources of Magnetic Field, Exercise 1: DPP

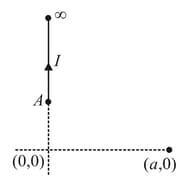
An infinitely long wire carrying current $I$ is along $Y$ axis such that its one end is at point $A \left(0, b\right)$ while the wire extends up to $+\infty$. The magnitude of magnetic field strength at Point $\left(a, 0\right)$ is found to be, $B=\frac{{\mu }_0}{4\mathrm{\pi }}\frac{i}{a}\left(n-\frac{b}{\sqrt{a^2+b^2}}\right)$. Find $n$.

Two parallel long wires carry currents $i_1$ and $i_2$ with $i_1>i_2.$ When the currents are in the same direction, the magnetic field midway between the wires is $10 \mathrm{\mu T}$. When the direction of $i_2$ is reversed, it becomes $40 \mathrm{\mu T}$. The ratio $i_1/i_2$ is

Two straight long conductors $AOB$ and $COD$ are perpendicular to each other and carry currents $i_1$ and $i_2.$ The magnitude of the magnetic induction at a point $P$ at a distance $a$ from the point $O$ in a direction perpendicular to the plane $ACBD$ is

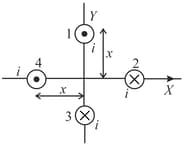
What will be the resultant magnetic field at origin due to four infinite length wires, if each wire produces magnetic field $\text{'}B\text{'}$ at origin

$AB$ and $CD$ are long straight conductor, distance $d$ apart, carrying a current $I$ The magnetic field at the midpoint of $BC$ is

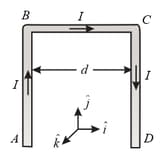
Figure shows a square loop $ABCD$ with edge length $a$. The resistance of the wire $ABC$ is $r$ and that of $ADC$ is $2r$. The value of magnetic field at the centre of the loop assuming uniform wire is

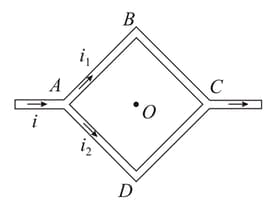
Two thick wires and two thin wires, all of the same materials and same length form a square in the three different ways $P$, $Q$ and $R$ as shown in the figure with current connection shown, the magnetic field at the centre of the square is zero in cases.

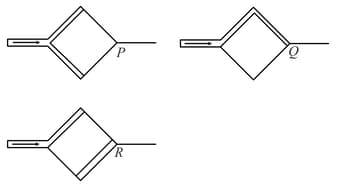
In the following figure, a wire bent in the form of a regular polygon of $n$ sides is inscribed in a circle of radius $a$. The net magnetic field at the center will be