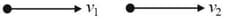B M Sharma Solutions for Chapter: Center of Mass, Exercise 4: DPP 1.4

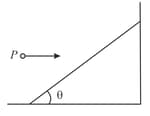
In the figure shown, a particle $P$ strikes the inclined smooth plane horizontally and rebounds vertically. If the angle $\text{θ}$ is $60°$ then, the coefficient of restitution is,

The smooth objects, with a coefficient of restitution $e$, collides directly and bounces as shown:

Just before impact   

Just after impact     

Newton's law of restitution gives,

A particle of mass $0.1 \mathrm{kg}$, moving with an initial speed $v$, collides with another particle of the same mass kept at rest. If after collision, total energy becomes $0.2 \mathrm{J}$, then,

A ball of mass $m$ approaches a wall of mass $M$$\left(\gg m\right)$ with speed $4\mathrm{ }\mathrm{m} {\mathrm{s}}^{-1}$ along the normal to the wall. The speed of wall is $1\mathrm{ }\mathrm{m} {\mathrm{s}}^{-1}$ towards the ball. The speed of the ball after an elastic collision with the wall will be,

A ball strikes a horizontal floor at an angle, $\text{θ}=45°$. The coefficient of restitution between the ball and the floor is, $e=\frac{1}{2}$. The fraction of its kinetic energy lost in the collision is,

In one-dimensional collision of two particles, the velocities interchanged when,
(i) collision is elastic and masses are unequal.
(ii) collision is inelastic but masses are unequal.
Select the correct alternative.

A particle of mass $m$ collides with a stationary particle and continues to move at an angle of $45°$ with respect to the original direction. The second particle also recoils at an angle of $45°$ to this direction. The mass of the second particle is (collision is elastic),

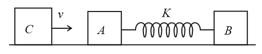
Two blocks $A$ and $B$, each of mass $m$,are connected to a massless spring of natural length $L$ and spring constant $K$. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length as shown in the figure. A third identical block $C$, also of mass $m$, moves on the floor with speed $v$ along the line joining $A$ and $B$ and collides elastically with $A$. Then,