B M Sharma Solutions for Chapter: Rigid Body Dynamics II, Exercise 4: DPP 3.4

A solid sphere of radius $R$ starts rotating on rough horizontal surface with translational velocity $V_0$ and initial angular velocity ${\omega }_0=\frac{2V_0}{3\mathrm{R}}$. The sphere starts pure rolling $3R$ after some time. Find the angle by which sphere rotates up to the instant at which pure rolling starts, if $V$ is the translational velocity at pure rolling. Assume uniformly accelerated motion upto start of pure rolling:

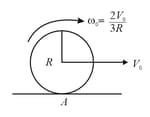
A solid sphere of radius $R$ starts rotating on rough horizontal surface with translational velocity $V_0$ and initial angular velocity ${\omega }_0=\frac{2V_0}{3\mathrm{R}}$. The sphere starts pure rolling $3R$ after some time. Assume uniformly accelerated motion upto start of pure rolling:

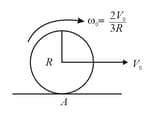
If $S$ is the distance covered by the sphere in rotational motion up to the instant at which pure rolling starts, find the velocity (translational) of the sphere during the pure rolling.

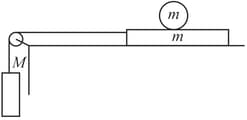
A plate of mass $m$ is placed on a frictionless surface. The plate is connected to a block of mass $M$ through a rope, over a massless pulley. A cylinder of mass $m$ is placed on the plate which rolls without slipping. Find the frictional force acting on the cylinder.

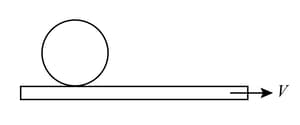
 A solid sphere of mass $m$ and radius $r$ is gently placed on a conveyer belt moving with constant velocity $V$. If the coefficient of friction between the belt and sphere is $\frac{2}{7}$, the distance travelled by the centre of the sphere before it starts pure rolling is

The string of a step rolling wheel is pulled by applying force $F$ with different lines of action in two situations as shown. The wheel starts rolling without slipping due to application of the force.

A solid sphere, a hollow sphere and a disc, all having same mass and radius are placed at the top of an incline and released. The friction coefficients between the objects and the incline are the same and not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by

A solid sphere, a hollow sphere and a disc, all having same mass and radius are placed at the top of an incline and released. The friction coefficients between the objects and the incline are the same and not sufficient to allow pure rolling. The smallest kinetic energy at the bottom of the incline will be achieved by:

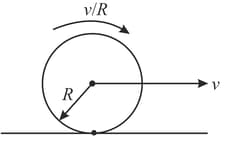
A disc is performing pure rolling on a smooth stationary surface with constant angular velocity as shown in the figure. At any instant, for the lowermost point of the disc