B M Sharma Solutions for Chapter: Linear and Angular Simple Harmonic Motion, Exercise 4: Archives

If $\mathrm{x},\mathrm{v} \mathrm{and} \mathrm{a}$ denote the displacement, the velocity and the acceleration of a particle executing SHM, of time period $\mathrm{T}$, then, which of the following does not change with time$?$

A mass $M$, attached to a horizontal spring, executes s.h.m. with amplitude $A_1$. When the mass $M$ passes through its mean position then a smaller mass $m$ is placed over it and both of them move together with amplitude $A_2$. The ratio of $\left(\frac{A_1}{A_2}\right)$ is
 

The amplitude of a damped oscillator decreases to $0.9$ times its original magnitude is $5 \mathrm{s}$. In another $10 \mathrm{s}$ it will decrease to $\alpha$ times its original magnitude, where $\alpha$ equals

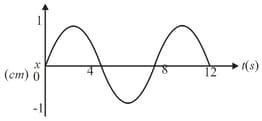
The $x-t$ graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at $t=\frac{4}{3} \mathrm{s}$ is

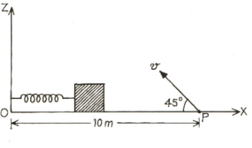
A small block is connected to one end of a massless spring of unstretched length $4.9 \mathrm{m}$. The other end of the spring is fixed as shown in the figure. The system lies on a horizontal frictionless surface. The block is stretched by $0.2 \mathrm{m}$  and released from rest at $\mathrm{t}=0$. lt then executes simple harmonic motion with angular frequency. $\mathrm{\omega }=\frac{\mathrm{\pi }}{3} \mathrm{rad}/\mathrm{s}$. Simultaneously at $\mathrm{t}=0$, a small pebble is projected with speed $\mathrm{v}$ from  point $\mathrm{P}$ at an angle of $45°$ as shown in the figure. Point P is at a horizontal distance of $10 \mathrm{m} \mathrm{from} \mathrm{O}$. If the pebble hits the block at $\mathrm{t}=1 \sec$, the value of $v$ is $:$
(take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$ )

A particle of mass $m$ is attached to one end of a massless spring of force constant$\mathrm{k}$, lying on a frictionless horizontal plane. The other end of the spring is fixed. The particle starts moving horizontally from its equilibrium position at time $\mathrm{t}=0$ with an initial velocity ${\mathrm{u}}_0$ when the speed of the particle is $0.5{\mathrm{u}}_0$ .It collides elastically with a rigid wall. After this collision.

A $0.1 \mathrm{kg}$ mass is suspended from a wire of negligible mass. The length of the wire is $1 \mathrm{m}$ and its cross-sectional area is $4.9\times {10}^{-7} {\mathrm{m}}^2$. If the mass is pulled a little in the vertically downward direction and released, it performs a simple harmonic motion of angular frequency $140 \mathrm{rad} {\mathrm{s}}^{-1}$. If Young's modulus of the material of the wire is $n\times {10}^9 \mathrm{N} {\mathrm{m}}^{-2}$, the value of $n$ is

A spring-block system is resting on a frictionless floor as shown in the figure. The spring constant is $2.0{\mathrm{Nm}}^{-1}$ and the mass of the block is $2.0 \mathrm{kg}$. Ignore the mass of the spring. Initially the spring is in an unstretched condition.