B M Sharma Solutions for Chapter: Linear and Angular Simple Harmonic Motion, Exercise 2: CONCEPT APPLICATION EXERCISE

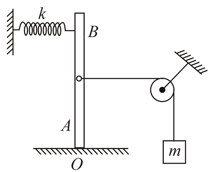
Two identical rods each of mass $m$ and length $L$, are rigidly joined and then suspended in a vertical plane so as to oscillate freely about an axis normal to the plane of paper passing through '$S$' (point of suspension). Find the time period of such small oscillations.

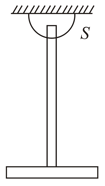
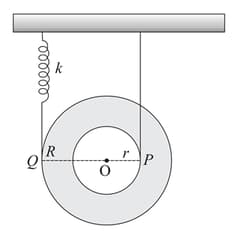
A stepped pulley having mass $m,$ radius $R$ and radius of gyration $k$ is connected with two ideal springs of stiffness $k$ and $k_2$ as shown in the figure. If the pulley rolls without sliding, find the angular frequency of its oscillation.

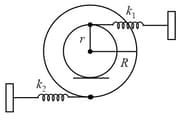
A stepped disc of mass $M$ and radius $R$ is pivoted at its center $C$ smoothly. An inextensible string connected with a light spring of stiffness $k$ passes over the pulley. One end of the string is rigidly connected with the ground and the other end is attached to a body of mass $m.$ If the string does not slide on the pulley, find the angular frequency of oscillation of the system.

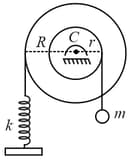
A disc of mass $m$ hanged by a string is attached at $P$ and a spring of stiffness $k$ is attached at $O.$ Find the frequency of small angular oscillation of the disc if the string does not slide over the pulley. Assume $I_0=MI$ of the disc about $O.$

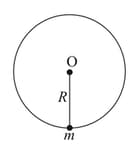
A disc of mass $M=2 \mathrm{m}$ and radius $R$ is pivoted at its centre. The disc is free to rotate in the vertical plane about its horizontal axis through its centre $O.$ A particle of mass $m$ is stuck on the periphery of the disc. Find the frequency of small oscillations of the system about its equilibrium position.

A square plate of mass $M$ and side length $L$ is hinged at one of its vertex $\left(A\right)$ and is free to rotate about it. Find the time period of small oscillations if

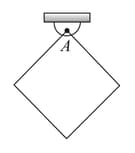
The plate performs oscillations in the verticai plane of the figure. (Axis is perpendicular to figure.)

A square plate of mass $M$ and side length $L$ is hinged at one of its vertex $\left(A\right)$ and is free to rotate about it. Find the time period of small oscillations if

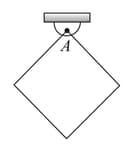
The plate performs oscillations about a horizontal axis passing through $A$ lying in the plane of the figure.

A massless road rigidly fixed at $O$. A string carrying a mass $m$ at one end is attached to point $A$ on the rod so that $OA=a$. At another point $B\left(OB=b\right)$ pf the rod, a horizontal spring of force constant $k$ is attached as shown. Find the period of small vertical oscillations of mass $m$ around its equilibrium position