BM Sharma Solutions for Chapter: Newton's Laws of Motion II, Exercise 3: DPP

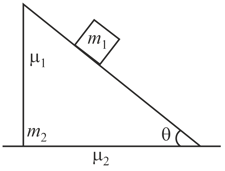
A block of mass $m_1$ is placed on a wedge of an angle $\mathrm{\theta }$, as shown. The block is moving over the inclined surface of the wedge. The friction coefficient between the block and the wedge is ${\mathit{\text{μ}}}_1$, whereas it is ${\mathit{\text{μ}}}_2$ between the wedge and the horizontal surface. If ${\mathit{\text{μ}}}_1=\frac{1}{2},\mathrm{\theta }=45°,m_1=4\mathrm{kg},m_2=5\mathrm{kg}$ and $g=10\mathrm{ }\mathrm{m} {\mathrm{s}}^{-2}$, find the minimum value of ${\mathit{\text{μ}}}_2$, so that the wedge remains stationary on the surface.

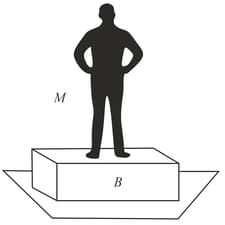
As shown in the figure, $M$ is a man of mass $60 \mathrm{kg}$ standing on a block of mass $40 \mathrm{kg}$ kept on the ground. The coefficient of friction between the feet of the man and the block is $0.3$ and that between $B$ and the ground is $0.1$. If the man accelerates with an acceleration $2 \mathrm{m} {\mathrm{s}}^{-2}$ in the forward direction, then

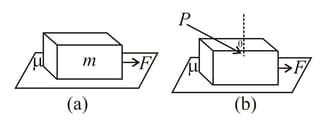
The coefficient of friction between the block and the horizontal surface is $\mathit{\text{μ}}$. The block moves towards right under the action of horizontal force $F$, as in the figure $\left(a\right)$. Sometime later, another force $P$ is also applied to the block making an angle $\mathrm{\theta }$ (such that $\tan \left(\mathrm{\theta }\right)=\mathit{\text{μ}}$) with vertical, as shown in figure $\left(b\right)$. After the application of force $P$, the acceleration of block shall

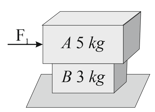
In the figure shown, if friction coefficient of blocks $1$ and $2$ with an inclined plane is $\mathit{\text{μ}}=0.5$ and $0.4$, respectively, then find the correct statement.

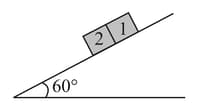
A force $F\mathit{=}\mathit{2}t$ (where $t$ is time in $\mathrm{seconds}$) is applied at $t=0 \sec$ to the block of mass $m$ placed on a rough horizontal surface. The coefficient of static and kinetic friction between the block and surface are ${\text{μ}}_{\mathit{s}}$and ${\text{μ}}_{\mathrm{k}}$, respectively. Which of the following graphs best represent the acceleration vs time of the block $({\text{μ}}_{\mathrm{s}}>{\text{μ}}_{\mathrm{k}})$?

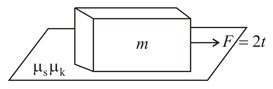
A block $A (5 \mathrm{kg})$ rests over another block $B\mathit{ }(3 \mathrm{kg})$ placed over a smooth horizontal surface. There is friction between $A$ and $B$. A horizontal force $F_1$, gradually increasing from zero to a maximum, is applied to $A$, so that the blocks move together without relative motion. Instead of this, another horizontal force $F_2$, gradually increasing from zero to a maximum, is applied to $B$, so that the blocks move together without relative motion. Then,