M L Aggarwal Solutions for Chapter: Surface Areas and Volumes, Exercise 7: Chapter Test

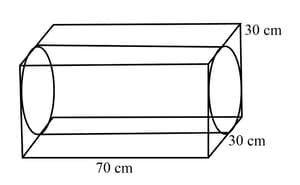
The figure given below, shows a cuboidal block of wood through which a circular cylindrical hole of the biggest size is drilled. Find the volume of the wood left in the block.

The figure given below shows a solid trophy made of shining glass. If one cubic centimetre of glass costs $₹ 0.75$, find the cost of the glass for making the trophy.

A solid wooden toy is in the shape of a right circular cone mounted on a hemisphere. If the radius of the hemisphere is $4.2 \mathrm{cm}$ and the total height of the toy is $10.2 \mathrm{cm}$, find the volume of the toy. (Use $\mathrm{\pi }=\frac{22}{7}$)

A solid metallic sphere of diameter $21 \mathrm{cm}$ is melted and recast into a number of smaller cones, each of diameter $7 \mathrm{cm}$ and height $3 \mathrm{cm}$. Find the number of cones so formed.

Water flows through a cylindrical pipe, whose inner radius is $1 \mathrm{cm}$, at the rate of $80 \mathrm{cm}/\sec$ in an empty cylindrical tank, the radius of whose base is $40 \mathrm{cm}$. What is the rise of water level in the tank in half an hour?

An open metal bucket is in the shape of a frustum of a cone of height $21 \mathrm{cm}$ with radii of its lower and upper ends as $10 \mathrm{cm}$ and $20 \mathrm{cm}$ respectively. Find the cost of milk which can completely fill the bucket at $₹ 30$ per litre.

A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is $24 \mathrm{cm}$ and diameters of its upper and lower circular ends are $30 \mathrm{cm}$ and $10 \mathrm{cm}$ respectively. Find the cost of metal sheet used in it at the rate of $₹ 10$ per $100 {\mathrm{cm}}^2$. (Use $\mathrm{\pi }=3.14$ )

A solid is in the shape of a frustum of a cone. The diameters of the two circular ends are $60 \mathrm{cm}$ and $36 \mathrm{cm}$ and the height is $9 \mathrm{cm}$. Find the area of its whole surface and the volume. (You can leave the answer in $\mathrm{\pi }$ )