Stefan-Boltzmann Law

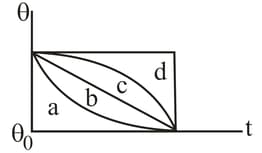
A hot liquid is kept in a big room. Its temperature is plotted as a function of time. Which of the following curves may represent the plot?

Two identical metal balls, one at $T_1=300 \mathrm{K}$ and the other at $T_2=600 \mathrm{K}$, are kept at a distance of $1 \mathrm{m}$ in vacuum. Will the temperature equalized by radiation? Will the rate of heat gained by the colder sphere be proportional to $T_2^4-T_1^4$ as may be expected from the Stefan's law?

Why is the white dress more comfortable than a dark dress in summer?

A solid sphere and a hollow sphere of the same material and of equal radii are heated to the same temperature.

A heated body emits radiation which has maximum intensity near the frequency ${\nu }_0$. The emissivity of the material is $0.5$. If the absolute temperature of the body is doubled,

Two bodies $A$ and $B$, having equal surface areas, are maintained at temperatures $10°\mathrm{C}$ and $20°\mathrm{C}$. The thermal radiation emitted in a given time by $A$ and $B$ are in the ratio,

The thermal radiation emitted by a body is proportional to $T^{\mathrm{n}}$ where $T$ is its absolute temperature. The value of $n$ is exactly $4$ for,

A solid at temperature $T_1$ is kept in an evacuated chamber at temperature $T_2>T_1$. The rate of increase of temperature of the body is proportional to,

One end of a rod is of length $20\mathrm{cm}$ and is inserted into a furnace at $800\mathrm{K}$. The sides of the rod are covered with an insulating material and the other end emits radiation like a blackbody. The temperature of this end is $750\mathrm{K}$ in a steady state. The temperature of the surrounding air is $300\mathrm{K}$. Assuming radiation to be the only important mode of energy transfer between the surrounding end and the open end of the rod, find the thermal conductivity of the rod. Stefan's constant $\mathrm{\sigma }=6\cdot 0\times {10}^{-8}{\mathrm{Wm}}^{-2}{\mathrm{K}}^{-4}$.

A cylindrical rod of length $50 \mathrm{cm}$ and cross sectional area $1{\mathrm{cm}}^2$ is fitted between a large ice chamber at $0°\mathrm{C}$ and an evacuated chamber maintained at $27°\mathrm{C}$ as shown in the figure. Only small portions of the rod are inside the chambers and the rest is thermally insulated from the surrounding. The cross-section fitted into the evacuated chamber is blackened so that it completely absorbs any radiation falling on it. The temperature of the blackened end is $17°\mathrm{C}$ when steady state is reached. Stefan's constant is $\sigma =6\times {10}^{-8}{\mathrm{Wm}}^{-2}{\mathrm{K}}^{-4}$. Find the thermal conductivity of the material of the rod.

A spherical ball $\mathrm{A}$ of surface area $20{\mathrm{cm}}^2$ is kept at the centre of a hollow spherical shell $\mathrm{B}$ of area $80{\mathrm{cm}}^2$. The surface of $\mathrm{A}$ and the inner surface of $\mathrm{B}$ emits black  bodies. Both $\mathrm{A} \mathrm{and} \mathrm{B}$ are at $300\mathrm{K}$.

(a) How much is the radiation energy emitted per second by the ball $\mathrm{A}?$

(b) How much is the radiation energy emitted per second by the inner surface of $\mathrm{B}$?

(c) How much of the energy emitted by the inner surface of $\mathrm{B}$ falls back on its surface itself?

A copper sphere is suspended in an evacuated chamber maintained at $300 \mathrm{K}$. The sphere is maintained at a constant temperature of $500 \mathrm{K}$ by heating it electrically. A total of $210 \mathrm{W}$ of electric power is needed to do it. When the surface of the copper sphere is completely blackened, $700 \mathrm{W}$ is needed to maintain the same temperature of the sphere. Calculate the emissivity of copper.

A cubical block of mass $1.0 \mathrm{kg}$ and edge $5.0 \mathrm{cm}$ is heated to $227°\mathrm{C}$. It is kept in an evacuated chamber maintained at $27°\mathrm{C}$. Assuming that the block emits radiation like a blackbody, find the rate at which the temperature of the block will decrease. The specific heat capacity of the material of the block is $400 \mathrm{J} {\mathrm{kg}}^{-1} {\mathrm{K}}^{-1}$.

A spherical tungsten piece of radius $1.0 \mathrm{cm}$ is suspended in an evacuated chamber maintained at $300\mathrm{K}$. The piece is maintained at a temperature of $1000\mathrm{K}$ by heating it electrically. Find the rate at which the electrical energy must be supplied. The emissivity of tungsten is $0.30$ and the Stefan constant $\mathrm{\sigma }$ is $6.0\times {10}^{-8} {\mathrm{Wm}}^{-2}{\mathrm{K}}^{-4}$.

A spherical ball of surface area $20 {\mathrm{cm}}^2$ absorbs any radiation that falls on it. It is suspended in a closed box maintained at $57°\mathrm{C}$.

 (a) Find the amount of radiation falling on the ball per second.

(b) Find the net rate of heat flow to or from the ball at an instant when its temperature is $200°\mathrm{C}$.

Stefan constant = $6·0\times {10}^{-8} {\mathrm{Wm}}^{-2}{\mathrm{K}}^{-4}$.

A $100 \mathrm{W}$ bulb has tungsten filament of total length $1.0 \mathrm{m}$ and radius $4\times {10}^{-5} \mathrm{m}$. The emissivity of the filament is $0·8$ and $\sigma =6·0\times {10}^{-8} \mathrm{W} {\mathrm{m}}^{-2} {\mathrm{K}}^{-4}$. Calculate the temperature of the filament when the bulb is operating at correct wattage.

A solid aluminium sphere and a solid copper sphere of twice the radius are heated to the same temperature and are allowed to cool under identical surrounding temperatures. Assume that the emissivity of both the spheres is the same. Find the ratio of $\left(\mathrm{a}\right)$ the rate of heat loss from the aluminium sphere to the rate of heat loss from the copper sphere $\left(\mathrm{b}\right)$ the rate of fall of aluminum sphere to the rate of fall of temperature of the copper sphere. The specific heat capacity of aluminium$=900 \mathrm{J} {\mathrm{kg}}^{-1} °{\mathrm{C}}^{-1}$ and that of copper$=390 \mathrm{J} {\mathrm{kg}}^{-1} °{\mathrm{C}}^{-1}$. The density of copper$=3.4$ times the density of aluminium.

Calculate the amount of heat radiated per second by a body surface area $12 {\mathrm{cm}}^2$ kept in thermal equilibrium in a room at temperature $20 °\mathrm{C}$. The emissivity of the surface $=0.80, \sigma =6.0\times {10}^{-8} \mathrm{W} {\mathrm{m}}^{-2 }{\mathrm{K}}^{-4}$. 

Assume that the total surface area of a human body is $1.6 {\mathrm{m}}^2$ and that it radiates like an ideal radiator. Calculate the amount of energy radiated per second by the body if the body temperature is $37 °\mathrm{C}$. Stefan constant $\sigma$ is $6.0\times {10}^{-8} \mathrm{W} {\mathrm{m}}^{-2} {\mathrm{K}}^{-4}$.