Relation Between Cp and Cv for an Ideal Gas

An ideal gas having the density $1.7\times {10}^{-3} \mathrm{g} {\mathrm{cm}}^{-3}$ at pressure $1.5\times {10}^5 \mathrm{Pa}$ is filled in a Kundt tube. When the gas is resonated at a frequency of $3.0 \mathrm{kHz}$, nodes are formed at a separation of $6.0 \mathrm{cm}$. Calculate the molar heat capacities $C_{\mathrm{P}}$ and $C_{\mathrm{V}}$ of the gas.

Standing waves of frequency $5.0 \mathrm{kHz}$ are produced in a tube filled with oxygen at $300 \mathrm{K}$. The separation between the consecutive nodes is $3.3 \mathrm{cm}$. Calculate the specific heat capacities $C_{\mathrm{P}} \mathrm{and} C_{\mathrm{V}}$ of the gas.

A mixture contains $1 \mathrm{mol}$ of helium $\left(C_{\mathrm{p}}=2.5R, C_{\mathrm{V}}=1.5R\right)$ and $1 \mathrm{mol}$ of hydrogen $\left(C_{\mathrm{p}}=3.5R, C_{\mathrm{V}}=2.5R\right)$. Calculate the values of $C_{\mathrm{p}}$, $C_{\mathrm{V}}$ and $\mathrm{\gamma }$ for the mixture.

Two ideal gases have the same value of $\frac{C_{\mathrm{p}}}{C_{\mathrm{V}}}=\mathrm{\gamma }$. What will be the value of this ratio for a mixture of the two gases in the ratio $1 : 2$?

An ideal gas $\left(C_{\mathrm{p}}/C_{\mathrm{V}}=\gamma \right)$ is taken through a process in which the pressure and the volume vary as $p=a{V}^{\mathrm{b}}$. Find the value of $b$ for which the specific heat capacity in the process is zero.

An ideal gas is taken through a process in which the pressure and the volume are changed according to the equation $p=kV$. Show that the molar heat capacity of the gas for the process is given by $C=C_{\mathrm{V}}+\frac{R}{2}$.

An amount $Q$ of heat is added to a monatomic ideal gas in a process in which the gas performs a work $\frac{\mathrm{Q}}{2}$ on its surrounding. Find the molar heat capacity for the process.

An ideal gas expands from $100 {\mathrm{cm}}^3$ to $200 {\mathrm{cm}}^3$ at a constant pressure of $2.0\times {10}^5 \mathrm{Pa}$ when $50 \mathrm{J}$ of heat is supplied to it. Calculate

(a) the change in internal energy of the gas.

(b) the number of moles in the gas if the initial temperature is $300 \mathrm{K}$.

(c) the molar heat capacity $C_{\mathrm{p}}$ at constant pressure.

(d) the molar heat capacity $C_{\mathrm{V}}$ at constant volume.

A sample of air weighing $1.18\mathrm{g}$ occupies $1.0\times {10}^3{\mathrm{cm}}^3$ when kept at $300 \mathrm{K}$ and $1.0\times {10}^5\mathrm{Pa}$. When $2.0\mathrm{cal}$ of heat is added to it at constant volume, its temperature increases by $1 °\mathrm{C}$. Calculate the amount of heat needed to increase the temperature of air by $1 °\mathrm{C}$ at constant pressure if the mechanical equivalent of heat is $4.2\times {10}^{-7} \mathrm{erg} {\mathrm{cal}}^{-1}$. Assume that air behaves as an ideal gas.

The specific heat capacities of hydrogen at constant volume and at constant pressure are $2.4\mathrm{cal}{\mathrm{g}}^{-1}°{\mathrm{C}}^{-1}$ and $3.4\mathrm{cal}{\mathrm{g}}^{-1}°{\mathrm{C}}^{-1}$, respectively. The molecular weight of hydrogen is $2\mathrm{g}{\mathrm{mol}}^{-1}$ and the gas constant $R=8.3\times {10}^7\mathrm{erg}°{\mathrm{C}}^{-1}{\mathrm{mol}}^{-1}$. Calculate the value of $J$.

A rigid container of negligible heat capacity contains one mole of an ideal gas. The temperature of the gas increases by $1°\mathrm{C}$ if $3.0 \mathrm{cal}$ of heat is added to it. The gas may be 

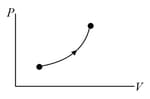
The molar heat capacity for the process shown in figure  is

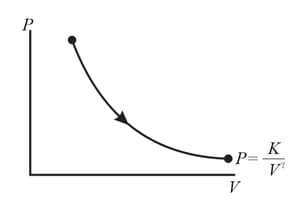
Figure shows a process on a gas in which pressure and volume both change. The molar heat capacity for this process is $C$.

$70$ calories of heat is required to raise the temperature of $2 \mathrm{moles}$ of an ideal gas at constant pressure from $30 °\mathrm{C}$ to $35 °\mathrm{C}$. The amount of heat required to raise the temperature of the same gas through the same range at constant volume is 

Let $C_{\mathrm{V}}$ and $C_{\mathrm{p}}$ denote the molar heat capacities of an ideal gas at constant volume and constant pressure respectively. Which of the following is a universal constant?

The value of $C_P-C_{\mathit{V}}$ is $1.00 R$ for a gas sample in state $A$ and is $1.08R$ in state $B$. Let $p_A, p_B$ denote the pressure and $T_A$ and $T_B$ denote the temperatures of states $A$ and $B$, respectively. Most likely

For a solid with a small expansion coefficient, 

The ratio $C_{\mathrm{p}}/C_{\mathrm{V}}$ for a gas is $1.29$. What is the degree of freedom of the molecules of this gas? 

In a real gas the internal energy depends on temperature and also on volume. The energy increases when the gas expands isothermally. Looking into the derivation of $C_{\mathrm{p}}-C_{\mathrm{V}}=R$, find whether $C_{\mathrm{p}}-C_{\mathrm{V}}$ will be more than $R$, less than $R$ or equal to $R$ for a real gas.

Does a solid also have two kinds of molar heat capacities $C_{\mathrm{p}}$ and $C_{\mathrm{V}}$? If yes, do we have $C_{\mathrm{p}}>C_{\mathrm{V}}$? Is $C_{\mathrm{p}}-C_{\mathrm{V}}=R$?