Karen Morrison and Nick Hamshaw Solutions for Exercise 9: Exercise 18.9
Karen Morrison Mathematics Solutions for Exercise - Karen Morrison and Nick Hamshaw Solutions for Exercise 9: Exercise 18.9
Attempt the free practice questions from Exercise 9: Exercise 18.9 with hints and solutions to strengthen your understanding. Cambridge IGCSE® Mathematics Core and Extended Coursebook Second Edition solutions are prepared by Experienced Embibe Experts.
Questions from Karen Morrison and Nick Hamshaw Solutions for Exercise 9: Exercise 18.9 with Hints & Solutions
Bacteria multiply rapidly because a cell divides into two cells and then those two cells divide to each produce two more cells and so on. The growth rate is exponential and we can express the population of bacteria over time using the formula ( is the period of time).
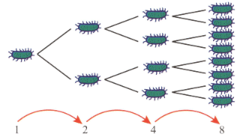
The graph shows the increase in bacteria numbers in a six-hour period.
How many bacteria are there after one hour?
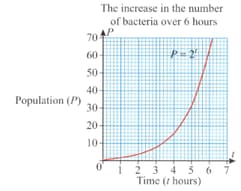
Bacteria multiply rapidly because a cell divides into two cells and then those two cells divide to each produce two more cells and so on. The growth rate is exponential and we can express the population of bacteria over time using the formula ( is the period of time).
The graph shows the increase in bacteria numbers in a six-hour period.
How long does it take for the number of bacteria to exceed cells?
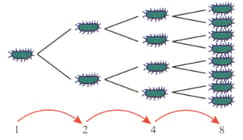
Bacteria multiply rapidly because a cell divides into two cells and then those two cells divide to each produce two more cells and so on. The growth rate is exponential and we can express the population of bacteria over time using the formula ( is the period of time).
The graph shows the increase in bacteria numbers in a six-hour period.
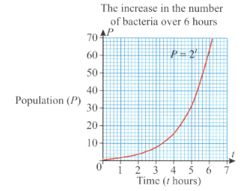
How many cells will there be after six hours?
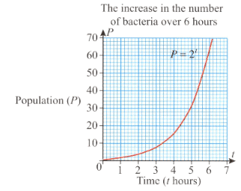
Bacteria multiply rapidly because a cell divides into two cells and then those two cells divide to each produce two more cells and so on. The growth rate is exponential and we can express the population of bacteria over time using the formula ( is the period of time).
The graph shows the increase in bacteria numbers in a six-hour period.
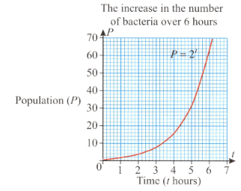
When would you expect the population to exceed one million bacteria if it continued to grow at this rate?
The temperature of metal in a smelting furnace increases exponentially as indicated in the following table.
Use the given data and plot the graph.
| Time (min) | |||||
| Temp |
The population of bedbugs in New York City is found to be increasing exponentially. The changes in population are given below.
Use the given data and answer the following question.
| Time (months) | |||||
| Population |
Plot the graph.
The population of bedbugs in New York City is found to be increasing exponentially. The changes in population are given below.
Use the given data and answer the following question.
| Time (months) | |||||
| Population |
When did the bedbug population reach ?
The population of bedbugs in New York City is found to be increasing exponentially. The changes in population are given below.
Use the given data and answer the following question.
| Time (months) | |||||
| Population |
What will the bedbug population be after six months if it continues to increase at this rate?
