Practical Applications of Connected Rates of Change
Important Questions on Practical Applications of Connected Rates of Change
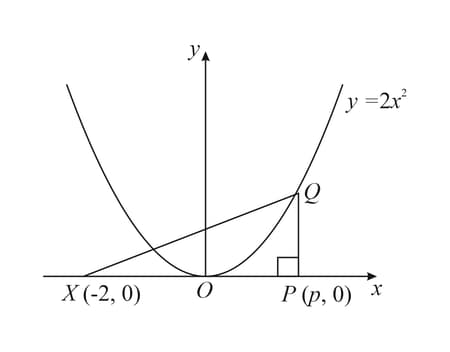
The diagram shows the curve and the points . The point lies on the curve and is parallel to the axis.
The point moves along the axis at a constant rate of units per second and moves along the curve so that remains parallel to the axis. Find the rate at which area increasing when .[Write your answer excluding units]
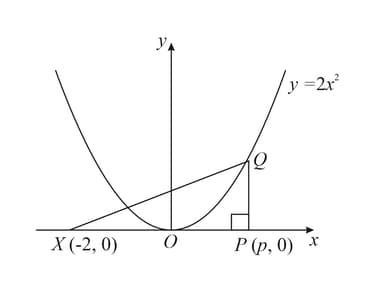
The diagram shows the curve and the points . The point lies on the curve and is parallel to the axis. Express area of triangle in terms of .
A watermelon is assumed to be spherical in shape while it is growing. Its mass, kg, and radius, cm, are related by the formula , where is a constant. It is also assumed that the radius is increasing at a constant rate of centimetres per day. On a particular day the radius is cm and the mass is kg. Find the value of and the rate at which the mass is increasing on this day.
An oil pipeline under the sea is leaking oil and a circular patch of oil has formed on the surface of the sea. At midday the radius of the patch of oil is m and is increasing at a rate of metres per hour. Find the rate at which the area of the oil is increasing at midday.
The volume of a spherical balloon is increasing at a constant rate of per second. Find the rate of increase of the radius of the balloon when the radius is cm.
The diagram shows a right circular cone with radius cm and height cm. The cone is initially completely filled with water. Water leaks out of the cone through a small hole at the vertex at a rate of . Find the rate of change of , when cm.
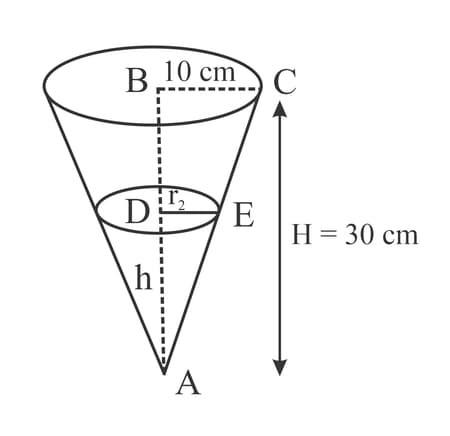
The diagram shows a right circular cone with radius cm and height cm. The cone is initially completely filled with water. Water leaks out of the cone through a small hole at the vertex at a rate of . Show that the volume of water in the cone, , when the height of the water is cm is given by the formula .
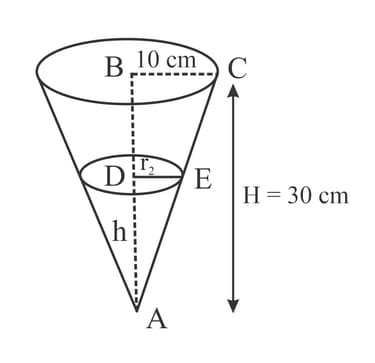
A cylindrical container of radius cm and height cm is completely filled with water. The water is then poured at a constant rate from the cylinder into an empty inverted cone.The cone has radius cm and height cm and its axis is vertical. It takes seconds for all of the water to be transferred. When the depth of the water in the cone is cm, Find the rate of change of the horizontal surface area of the water in the cone.
A cylindrical container of radius cm and height cm is completely filled with water. The water is then poured at a constant rate from the cylinder into an empty inverted cone.The cone has radius cm and height cm and its axis is vertical. It takes seconds for all of the water to be transferred. When the depth of the water in the cone is cm, find the rate of change of the height of the water in the cone.
A cylindrical container of radius cm and height cm is completely filled with water. The water is then poured at a constant rate from the cylinder into an empty inverted cone.The cone has radius cm and height cm and its axis is vertical. It takes seconds for all of the water to be transferred. If represents the volume of water, in , in the cone at time seconds, find in terms of .
Paint is poured onto a flat surface and a circular patch is formed. The area of the patch increases at a rate of . Find, in terms of , the rate of increase of the radius of the patch after seconds.
Paint is poured onto a flat surface and a circular patch is formed. The area of the patch increases at a rate of . Find, in terms of , the radius of the patch after seconds.
Oil is poured onto a flat surface and a circular patch is formed. The radius of the patch increases at a rate of . Find the rate at which the area is increasing when the circumference is .
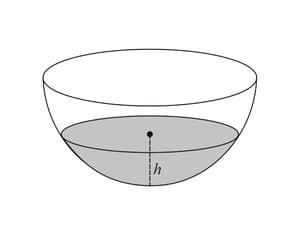
Water is poured into the hemispherical bowl of radius cm at a rate of . After seconds, the volume of water in the bowl, is given by , where cm is the height of the water in the bowl. Find the rate of change of when cm.
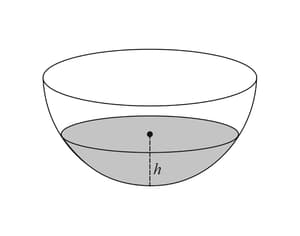
Water is poured into the hemispherical bowl of radius cm at a rate of . After seconds, the volume of water in the bowl, is given by , where cm is the height of the water in the bowl. Find the rate of change of when cm.
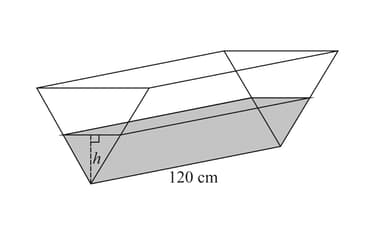
The diagram shows a water container in the shape of a triangular prism of length cm.The vertical cross-section is an equilateral triangle. Water is poured into the container at a rate of . Find the rate of change of when cm.
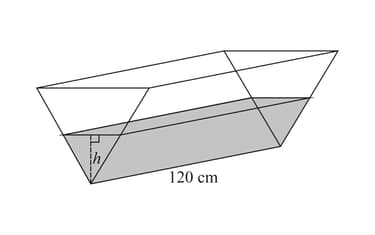
The diagram shows a water container in the shape of a triangular prism of length cm.The vertical cross-section is an equilateral triangle. Water is poured into the container at a rate of . Show that the volume of water in the container, , is given by , where cm is the height of the water in the container.
A closed circular cylinder has radius cm and surface area , where . Given that the radius of the cylinder is increasing at a rate of , find the rate of change of when cm.
A solid metal cuboid has dimensions .The cuboid is heated and the volume increases at a rate of . Find the rate of increase of when cm.
A cube has side length cm and volume . The volume is increasing at a rate of . Find the rate of increase of when .

