Jan Dangerfield, Stuart Haring and, Julian Gilbey Solutions for Exercise 9: END-OF-CHAPTER REVIEW EXERCISE 3

A boat is in equilibrium held by a rope to the shore. The rope exerts a force $T$ at an angle $\theta$ from north. The wind blows the boat with force $40 \mathrm{N}$ in a northwest direction. The current pushes it south with a force of $50 \mathrm{N}.$ Show that $T\sin \theta =20\sqrt{2}$ and find an expression for $T\cos \theta$. Hence, show that $\tan \theta =\frac{8+10\sqrt{2}}{17}$ and find $\theta$ and $T.$

A car of mass $300 \mathrm{kg}$ is on a slope, which is at an angle of $5°$ to the horizontal. When it is pulled down the slope by a rope parallel to the slope with a force of $T,$ it accelerates at $2 \mathrm{m}{ \mathrm{s}}^{-2}.$ Find the acceleration of the car when it is pulled up the slope by a rope parallel to the slope with a force of $T.$.

A girl can drag a stone block of mass $18 \mathrm{kg}$ up a slope at an angle of $13°$ to the horizontal with an acceleration of $0.7 \mathrm{m}{ \mathrm{s}}^{-2}.$ Assuming this is the maximum force she can exert to drag the block, find the mass of the heaviest stone block she would be able to drag up the slope.

A ball of mass $m \mathrm{kg}$ slides down a slope, which is at an angle of $\theta °$ to the horizontal. It passes two light gates $x\mathit{ }\mathrm{m}$ apart. At the first gate, the speed of the ball is measured as $u \mathrm{m}{ \mathrm{s}}^{-1},$ and at the second its speed is measured as $v \mathrm{m}{ \mathrm{s}}^{-1}.$ Assuming the resistance is constant, show the resistance force has a total size of $\frac{m}{2\mathrm{x}}\left(2\mathrm{xgsin}\theta +u^2-v^2\right).$

A car of mass $m \mathrm{kg}$ is rolling down a slope of length $x \mathrm{m},$ which is at an angle of $30°$ to the horizontal. It has a booster that provides a force of $mg \mathrm{N}$ over a distance of $1 \mathrm{m}$, which the driver sets off at a distance $s \mathrm{m},$ after the car starts moving. Assuming the booster is used before the end of the slope, show that the speed at the bottom of the slope is given by $v^2=g(x+2)$ and deduce that the final speed is independent of when the booster is applied. (Note that if the booster were applied for a fixed time rather than a fixed distance this would not be true.)

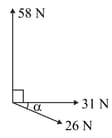
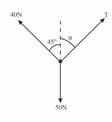
Coplanar forces of magnitudes $58 \mathrm{N}, 31 \mathrm{N}$ and $26 \mathrm{N}$ act at a point in the directions shown in the diagram. Given that $\tan \alpha =\frac{5}{12},$ find the magnitude and direction of the resultant of the three forces.

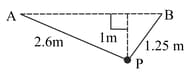
A particle $P$ of mass $1.05 \mathrm{kg}$ is attached to one end of each of two light inextensible strings, of lengths $2.6 \mathrm{m}$ and $1.25 \mathrm{~m}$. The other ends of the strings are attached to fixed points $A$ and $B$, which are at the same horizontal level. $P$ hangs in equilibrium at a point $1 \mathrm{~m}$ below the level of $A$ and $B$ (see diagram). Find the tensions in the strings.

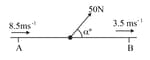
A block of mass $60 \mathrm{kg}$ is pulled up a hill in the line of greatest slope by a force of magnitude $50 \mathrm{N}$ acting at an angle $\alpha °$ above the hill. The block passes through points $A$ and $B$ with speeds $8.5 \mathrm{m}{ \mathrm{s}}^{-1}$ and $3.5 \mathrm{m}{ \mathrm{s}}^{-1}$ respectively (see diagram). The distance $AB$ is $250 \mathrm{m}$ and $B$ is $17.5 \mathrm{m}$ above the level of $A.$ The resistance to motion of the block is $6 \mathrm{N}.$ Find the value of $\alpha .$