Sue Pemberton Solutions for Chapter: Further Differentiation, Exercise 5: EXERCISE 8C
Sue Pemberton Mathematics Solutions for Exercise - Sue Pemberton Solutions for Chapter: Further Differentiation, Exercise 5: EXERCISE 8C
Attempt the practice questions on Chapter 8: Further Differentiation, Exercise 5: EXERCISE 8C with hints and solutions to strengthen your understanding. Cambridge International AS & A Level Mathematics : Pure Mathematics 1 Course Book solutions are prepared by Experienced Embibe Experts.
Questions from Sue Pemberton Solutions for Chapter: Further Differentiation, Exercise 5: EXERCISE 8C with Hints & Solutions
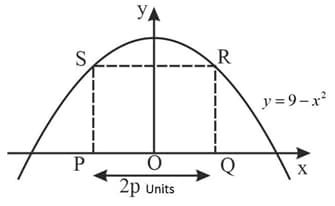
is a rectangle with base length units and area units2. The points and lie on the -axis and the points and lie on the curve . Find the value of for which has a stationary value.
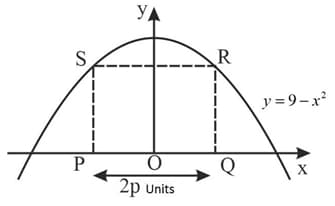
is a rectangle with base length units and area units2. The points and lie on the -axis and the points and lie on the curve . Find the value of for which has a stationary value. Find this stationary value and determine its nature.
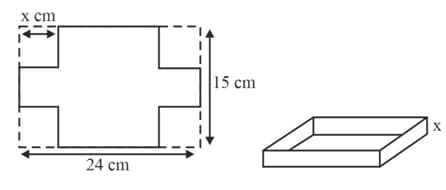
The diagram shows a by sheet of metal with a square of side removed from each corner. The metal is then folded to make an open rectangular box of depth and volume . Show that .
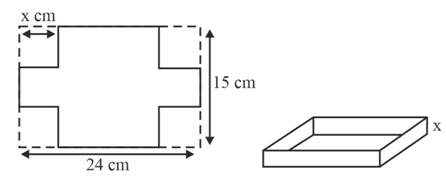
The diagram shows a by sheet of metal with a square of side removed from each corner. The metal is then folded to make an open rectangular box of depth and volume . Find the stationary value of and the value of for which this occurs.
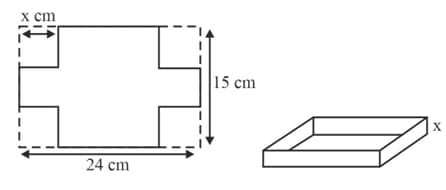
The diagram shows a by sheet of metal with a square of side removed from each corner. The metal is then folded to make an open rectangular box of depth and volume . Find the stationary value of and the value of for which this occurs. Determine the nature of this stationary value.
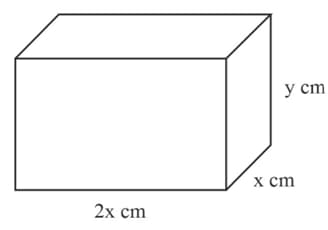
The volume of the solid cuboid shown in the diagram is and the surface area is . Express in terms of .
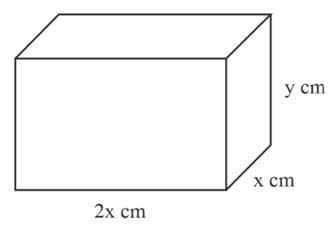
The volume of the solid cuboid shown in the diagram is and the surface area is . Show that
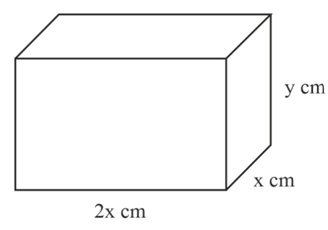
The volume of the solid cuboid shown in the diagram is and the surface area is . Find the minimum value of and state the dimensions of the cuboid for which this occurs.