The diagram shows part of the curve with parametric equations x = 2 ln ( t + 2 ) , y = t 3 + 2 t + 3 . At the point P on the curve, the value of the parameter is p . It is given that the gradient of the curve at P is 1 2 . Show that p = 1 3 p 2 + 2 - 2 . By first using an iterative formula p n + 1 = 1 3 p n 2 + 2 - 2 , determine the coordinates of the point P . Give the result of each iteration to 5 decimal places and each coordinate of P correct to 2 decimal places. [Use ln 0 . 08 = - 2 . 5257 ]

Given Parametric equations of a curve are x = 2 ln ( t + 2 ) , and y = t 3 + 2 t + 3 . We need to find the gradient of this curve at the origin. d x d t = d d t 2 ln t + 2 = 2 d d t ln t + 2 = 2 × 1 t + 2 × d d t t + 2 ∵ d d t ln t = 1 t , t > 0 = 2 t + 2 . . . . i ∵ d d t t n = n t n - 1 , n ∈ R Now, d y d t = d d t t 3 + 2 t + 3 = d d t t 3 + 2 d d t t + d d t 3 = 3 t 2 + 2 . . . . i i ∵ d d t t n = n t n - 1 , n ∈ R We know that when a curve is given in parametric form, in terms of the parameter t , we can use the chain rule to find d y d x in terms of t i.e., d y d x = d y d t × d t d x = 3 t 2 + 2 × t + 2 2 . . . . i It is given that at any point P on the curve, the value of the parameter is p . And, d y d x at point P is 1 2 . We need to show that p = 1 3 p 2 + 2 - 2 . Thus, using equation i , we have 1 2 = 3 p 2 + 2 p + 2 2 . . . . i i ⇒ p + 2 = 1 3 p 2 + 2 ⇒ p = 1 3 p 2 + 2 - 2 Hence, Proved. Now, let f p = 3 p 2 + 2 p + 2 - 1 = 3 p 3 + 6 p 2 + 2 p + 3 Also, f - 1 = 3 - 1 3 + 6 × - 1 2 + 2 × - 1 + 3 = - 3 + 6 - 2 + 3 = 4 > 0 f - 2 = 3 × - 2 3 + 6 × - 2 2 + 2 × - 2 + 3 = - 24 + 24 - 12 = - 12 < 0 ⇒ - 2 < p < - 1 Thus, now we need to find the roots of the function, f p using an iterative formula, p n + 1 = 1 3 p n 2 + 2 And, taking an initial approximation as, p 1 = - 1 . 5 p 1 = - 1 . 5 p n + 1 = 1 3 p n 2 + 2 - 2 Are these same correct to 2 decimal places. p 2 = 1 3 × - 1 . 5 2 + 2 - 2 = - 1 . 88571 No p 2 = 1 3 × - 1 . 88571 2 + 2 - 2 = - 1 . 92106 No p 3 = 1 3 × - 1 . 92106 2 + 2 - 2 = 1 13 . 07141 - 2 = - 1 . 92350 Yes Hence, the required value of p is - 1 . 92 correct to 2 decimal places.At point P , we have x = 2 ln p + 2 , and y = p 3 + 2 p + 3 Since p = - 1 . 92 ∴ x = 2 ln - 1 . 92 + 2 = 2 ln 0 . 08 = - 5 . 05 , and y = - 1 . 92 3 + 2 × - 1 . 92 + 3 = - 7 . 077888 - 3 . 84 + 3 = - 7 . 92 Hence, the required coordinates are - 5 . 05 , - 7 . 92

The equation of a curve is y = 3 x 2 x 2 + 4 . At the point on the curve with positive x -coordinate p , the gradient of the curve is 1 2 . Show that p = 48 p - 16 p 2 + 8 . Use an iterative formula p n + 1 = 48 p n - 16 p n 2 + 8 to find the value of p correct to 4 significant figures. Give the result of each iteration to 6 significant figures.

Given equation of the curve is y = 3 x 2 x 2 + 4 It is given that at x = p , we have d y d x = 1 2 then we need to show that p = 48 p - 16 p 2 + 8 . d y d x = d d x 3 x 2 x 2 + 4 = x 2 + 4 d d x 3 x 2 - 3 x 2 d d x x 2 + 4 x 2 + 4 2 ∵ d d x u v = u d v d x - v d u d x v 2 = x 2 + 4 × 3 × 2 x - 3 x 2 × 2 x x 2 + 4 2 ∵ d d x x n = n x n - 1 , n ∈ R = x 2 + 4 × 6 x - 6 x 3 x 2 + 4 2 = 6 x 3 + 24 x - 6 x 3 x 2 + 4 2 = 24 x x 2 + 4 2 Hence, d y d x = 24 x x 2 + 4 2 At x = p , we have d y d x = 1 2 ⇒ 1 2 = 24 p p 2 + 4 2 ⇒ p 2 + 4 2 = 48 p ⇒ p 4 + 8 p 2 + 16 = 48 p ⇒ p 4 + 8 p 2 = 48 p - 16 ⇒ p 2 = 48 p - 16 p 2 + 8 ⇒ p = 48 p - 16 p 2 + 8 [Since p > 0 ] Hence, Proved. Let f p = p 4 + 8 p 2 - 48 p + 16 ⇒ f 2 = 2 4 + 8 2 2 - 48 × 2 + 16 = 16 + 32 - 96 + 16 = - 32 < 0 f 3 = 3 4 + 8 × 3 2 - 48 × 3 + 16 = 81 + 72 - 144 + 16 = 25 > 0 Thus, the change of sign indicates that the value of p lies between 2 , and 3 . So, let us take our initial approximation as p 1 = 2 . 5 . Now, we need to use the iterative formula, p n + 1 = 48 p n - 16 p n 2 + 8 to find the value of p correct to 4 significant figures. p 1 = 2 . 5 p n + 1 = 48 p n - 16 p n 2 + 8 Are these same correct to 4 significant figures? p 2 = 48 × 2 . 5 - 16 2 . 5 2 + 8 = 104 14 . 25 = 2 . 70153 No p 3 = 48 2 . 70153 - 16 2 . 70153 2 + 8 = 113 . 67344 15 . 5842 = 7 . 2941447 = 2 . 70077 No p 4 = 48 × 2 . 70077 - 16 2 . 70077 2 + 8 = 113 . 63696 15 . 2942 = 7 . 43007 = 2 . 72582 No p 5 = 48 2 . 72582 - 16 2 . 72582 2 + 8 = 114 . 83936 15 . 430094 = 7 . 442557 = 2 . 72811 No p 6 = 48 2 . 72811 - 16 2 . 72811 2 + 8 = 114 . 94928 15 . 44258417 = 7 . 443655721 = 2 . 72831 Yes Hence, the required value of p correct to 3 significant figures is 2 . 728 .

By differentiating 1 cos θ , show that if y = sec θ then d y d θ = tan θ sec θ . Hence, show that d 2 y d θ 2 = a sec 3 θ + b se c θ , giving the values of a and b .

Given, y = sec θ = 1 cos θ = cos θ - 1 d y d θ = d d θ cos θ - 1 = - cos θ - 2 × d d θ cos θ [Applying the chain rule for differentiation] = - 1 cos 2 θ × - sin θ = 1 cos θ × sin θ cos θ = tan θ sec θ ∵ 1 cos θ = sec θ , a n d sin θ cos θ = tan θ Hence, d y d θ = d d θ sec θ = tan θ sec θ . . . . i Now, we need to prove: d 2 y d θ 2 = a sec 3 θ + b sec θ We know that d 2 y d θ 2 = d d θ d y d θ = d d θ tan θ sec θ [using i ] = tan θ d d θ sec θ + sec θ d d θ tan θ [Applying the Product rule in differentiation] = tan θ × tan θ sec θ + sec θ × sec 2 θ [Using i , and d d θ tan θ = sec 2 θ ] = tan 2 θ sec θ + sec 3 θ = sec 2 θ - 1 sec θ + sec 3 θ ∵ 1 + tan 2 θ = sec 2 θ = sec 3 θ - sec θ + sec 3 θ = 2 sec 3 θ - sec θ Hence, d 2 y d θ 2 = 2 sec 3 θ - sec θ or d 2 y d θ 2 = a sec 3 θ + b sec θ where a = 2 , and b = - 1 .

Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Cross-Topic Review Exercise 2, Exercise 1: CROSS-TOPIC REVIEW EXERCISE 2

Author:Sue Pemberton, Julianne Hughes & Julian Gilbey

Sue Pemberton Mathematics Solutions for Exercise - Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Cross-Topic Review Exercise 2, Exercise 1: CROSS-TOPIC REVIEW EXERCISE 2

Attempt the free practice questions on Chapter 15: Cross-Topic Review Exercise 2, Exercise 1: CROSS-TOPIC REVIEW EXERCISE 2 with hints and solutions to strengthen your understanding. Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book solutions are prepared by Experienced Embibe Experts.

Questions from Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Cross-Topic Review Exercise 2, Exercise 1: CROSS-TOPIC REVIEW EXERCISE 2 with Hints & Solutions

EASY

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 15 - Cross-Topic Review Exercise 2>CROSS-TOPIC REVIEW EXERCISE 2>Q 5

Use the trapezium rule with two intervals to estimate the value of $\int_{0}^{1} \frac{1}{6 + 2 e^{x}} d x$ , giving your answer correct to $2$ decimal places.

MEDIUM

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 15 - Cross-Topic Review Exercise 2>CROSS-TOPIC REVIEW EXERCISE 2>Q 23

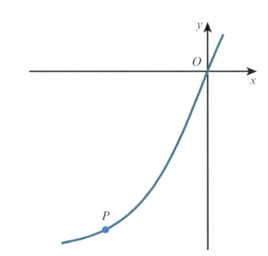
Question Image

The diagram shows part of the curve with parametric equations

$x = 2 \ln (t + 2), y = t^{3} + 2 t + 3 .$

At the point $P$ on the curve, the value of the parameter is $p$ . It is given that the gradient of the curve at $P$ is $\frac{1}{2}$ .

Show that $p = \frac{1}{3 p^{2} + 2} - 2 .$

By first using an iterative formula $p_{n + 1} = \frac{1}{(3 {p_{n}}^{2} + 2)} - 2$ , determine the coordinates of the point $P$ . Give the result of each iteration to $5$ decimal places and each coordinate of $P$ correct to $2$ decimal places. [Use $\ln (0.08) = - 2.5257$ ]

MEDIUM

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 15 - Cross-Topic Review Exercise 2>CROSS-TOPIC REVIEW EXERCISE 2>Q 25

Prove the identity $\cos 4 θ + 4 \cos 2 θ = 8 \cos^{4} θ - 3$ . Hence, find the exact value of $\int_{0}^{\frac{π}{4}} \cos^{4} θ d θ$ .

MEDIUM

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 15 - Cross-Topic Review Exercise 2>CROSS-TOPIC REVIEW EXERCISE 2>Q 26

By first expanding $\cos (2 x + x)$ , show that $\cos 3 x = 4 \cos^{3} x - 3 \cos x$ . Hence, show that $\int_{0}^{\frac{π}{6}} (2 \cos^{3} x - \cos x) d x = \frac{5}{12}$ .

MEDIUM

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 15 - Cross-Topic Review Exercise 2>CROSS-TOPIC REVIEW EXERCISE 2>Q 27

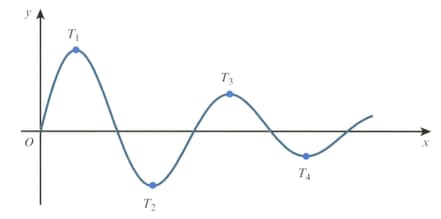
Question Image

The diagram shows the curve $y = 10 e^{- \frac{1}{2} x} \sin 4 x$ for $x ⩾ 0$ . The stationary points are labelled $T_{1}, T_{2}, T_{3}, \dots$ as shown.

It is given that the $x$ -coordinate of $T_{n}$ is greater than $25$ . Find the least possible value of $n$ .

EASY

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 15 - Cross-Topic Review Exercise 2>CROSS-TOPIC REVIEW EXERCISE 2>Q 28

The equation of a curve is $y = \frac{3 x^{2}}{x^{2} + 4}$ . At the point on the curve with positive $x$ -coordinate $p$ , the gradient of the curve is $\frac{1}{2} .$

Show that $p = \sqrt{(\frac{48 p - 16}{p^{2} + 8})}$ .

HARD

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 15 - Cross-Topic Review Exercise 2>CROSS-TOPIC REVIEW EXERCISE 2>Q 28

The equation of a curve is $y = \frac{3 x^{2}}{x^{2} + 4}$ . At the point on the curve with positive $x$ -coordinate $p$ , the gradient of the curve is $\frac{1}{2} .$

Show that $p = \sqrt{(\frac{48 p - 16}{p^{2} + 8})}$ .

Use an iterative formula $p_{n + 1} = \sqrt{(\frac{48 p_{n} - 16}{{p_{n}}^{2} + 8})}$ to find the value of $p$ correct to $4$ significant figures. Give the result of each iteration to $6$ significant figures.

MEDIUM

AS and A Level

IMPORTANT

Cambridge International AS & A Level Mathematics : Pure Mathematics 2 & 3 Course Book>Chapter 15 - Cross-Topic Review Exercise 2>CROSS-TOPIC REVIEW EXERCISE 2>Q 29

By differentiating $\frac{1}{\cos θ}$ , show that if $y = \sec θ$ then $\frac{d y}{d θ} = \tan θ \sec θ$ . Hence, show that $\frac{d^{2} y}{d θ^{2}} = a \sec^{3} θ + b se c θ$ , giving the values of $a$ and $b$ .

Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Cross-Topic Review Exercise 2, Exercise 1: CROSS-TOPIC REVIEW EXERCISE 2

Sue Pemberton Mathematics Solutions for Exercise - Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Cross-Topic Review Exercise 2, Exercise 1: CROSS-TOPIC REVIEW EXERCISE 2

Questions from Sue Pemberton, Julianne Hughes and, Julian Gilbey Solutions for Chapter: Cross-Topic Review Exercise 2, Exercise 1: CROSS-TOPIC REVIEW EXERCISE 2 with Hints & Solutions

Learn and Prepare for any exam you want !