Linear Programming Problems

Children have been invited to a birthday party. It is necessary to give them return gifts. For this purpose, it was decided that they would be given pens and pencils in a bag. It was also decided that the number of items in a bag would be at least $5.$ If the cost of a pen is $\mathrm{Rs} 10$ and cost of a pencil is $\mathrm{Rs} 5,$ minimize the cost of a bag containing pens and pencils. Formulation of LPP for this problem is

A printing company prints two types of magazines $A$ and $B.$ The company earns $\mathrm{Rs} 10$ and $\mathrm{Rs} 15$ on each magazine $A$ and $B$, respectively. These are processed on three machines $\mathrm{I},\mathrm{II} \&\hspace{0.17em}\mathrm{III}$ and total time in hours available per week on each machine is as follows:

In equation $y-x\le 0$ represents

Which of the following cannot be considered as the objective function of a linear programming problem?

A company manufactures two types of products $A$ and $B.$ The storage capacity of its godown is $100$ units. Total investment amount is $\mathrm{Rs} 30,000.$ The cost price of $A$ and $B$ are $\mathrm{Rs} 400$ and $\mathrm{Rs} 900$, respectively. Suppose all the products have sold and per-unit profit is $\mathrm{Rs} 100$ and $\mathrm{Rs} 120$ through $A$ and $B$, respectively. If $x$ units of $A$ and $y$ units of $B$ be produced, then two linear constraints and iso-profit line are respectively

A linear programming problem of linear functions deals with

The graph of inequations $x\le y$ and $y\le x+3$ is located in

The value of objective function is maximum under linear constraints is

A wholesale merchant wants to start the business of cereal with $\mathrm{Rs} 24000.$ Wheat is $\mathrm{Rs} 400$ per quintal and rice is $\mathrm{Rs} 600$ per quintal. He has capacity to store $200$ quintal cereal. He earns the profit $\mathrm{Rs} 25$ per quintal on wheat and $\mathrm{Rs} 40$ per quintal on rice. If he store $x$ quintal rice and $y$ quintal wheat, then for maximum profit, the objective function is

For the constraint of a linear optimising function $z=x_1+x_2,$ given by $x_1+x_2\le 1, 3x_1+x_2\ge 3$ and $x_1, x_2\ge 0$.

Corner points of the feasible region for an LPP are $\left(0,2\right),\left(3,0\right),\left(6,0\right),\left(6,8\right)$ and  $\left(0,5\right)$. Let $F=4x+6y$ be the objective function. Then, the minimum value of $F$ occurs at

Region represented by $x\ge 0, y\ge 0$ is

The feasible region for an LPP is shown shaded in the figure. Let, $Z=3x-4y$ be the objective function. Then, minimum of $Z$ occurs at

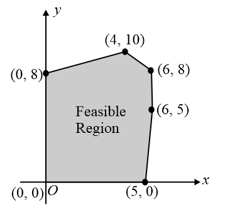
Objective function of a L.P.P. is

L.P.P. has constraints of

L.P.P is a process of finding